Câu hỏi:
11/07/2024 4,064
Chứng minh rằng biểu thức P = (2y ‒ x)(x + y) + x(y ‒ x) ‒ 2y(x + 5y) ‒ 1 luôn nhận giá trị âm với mọi giá trị của biến x và y.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Ta có:
P = (2y ‒ x)(x + y) + x(y ‒ x) ‒ 2y(x + 5y) ‒ 1
= 2xy + 2y2 ‒ x2 ‒ xy + xy ‒ x2 ‒ 2xy ‒ 10y2 ‒ 1
= (2xy – xy + xy – 2xy) + (2y2 ‒ 10y2) + (‒ x2 ‒ x2) – 1
= ‒8y2 ‒ 2x2 ‒ 1.
Do với mọi giá trị của x, y ta có: x2 ≥ 0, y2 ≥ 0 nên ‒ 2x2 ≤ 0, ‒8y2 ≤ 0
Suy ra ‒8y2 ‒ 2x2 ‒ 1 ≤ ‒1 với mọi giá trị của biến x, y.
Vậy P luôn nhận giá trị âm với mọi giá trị của biến x và y.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
a) Ta có:
M = (x ‒ 1)(x2 + x + 1) ‒ x2(x ‒ 1) ‒ x2 ‒ 23
= x3 + x2 + x ‒ x2 ‒ x ‒ 1 ‒ x3 + x2 ‒ x2 ‒ 23
= (x3 ‒ x3) + (x2 ‒ x2) + (x ‒ x) + (‒1 ‒ 23)
= ‒24.
Vậy giá trị của M không phụ thuộc vào giá trị của biến.
b) Ta có:
\(N = \left( {x - \frac{1}{2}y} \right)\left( {{x^2} + 2y} \right) - x\left( {{x^2} + 2y} \right) + y\left( {\frac{1}{2}{x^2} + y} \right) - \frac{1}{2}\)
\(\; = {x^3} + 2xy - \frac{1}{2}{x^2}y - {y^2} - {x^3} - 2xy + \frac{1}{2}{x^2}y + {y^2} - \frac{1}{2} = - \frac{1}{2}{\rm{.\;}}\)
Vậy giá trị của N không phụ thuộc vào giá trị của biến.
Lời giải
Lời giải
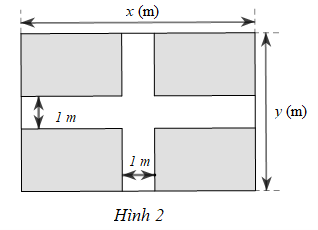
a) Phần còn lại của mảnh đất gồm bốn miếng đất bằng nhau có dạng hình chữ nhật với chiều dài bằng \(\frac{{x - 1}}{2}\left( {\rm{m}} \right)\), chiều rộng bằng \(\frac{{y - 1}}{2}\left( {\rm{m}} \right)\).
Vậy đa thức biểu thị diện tích phần còn lại của mảnh đất đó là:
\(S = 4 \cdot \frac{{x - 1}}{2} \cdot \frac{{y - 1}}{2} = xy - x - y + 1\,\,\left( {{{\rm{m}}^2}} \right)\).
b) Thay x = 9; y = 5,4 vào S ta có:
S = 9.5,4 – 9 – 5,4 + 1 = 48,6 – 9 – 5,4 + 1 = 35,2 (m2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
10 Bài tập Nhận biết đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn thức (có lời giải)
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
-
Dạng 8: Bài luyện tập 3 dạng 4. Tổng hợp có đáp án
-
Dạng 2: Bài luyện tập 1 Dạng 2: Rút gọn phân thức có đáp án