Câu hỏi:

03/07/2023 747

Cho hình nón đỉnh S có đường cao SO = a. Một mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách từ O đến mặt phẳng (SAB) bằng \(\frac{{a\sqrt 2 }}{2}\). Diện tích xung quanh của hình nón đã cho bằng

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

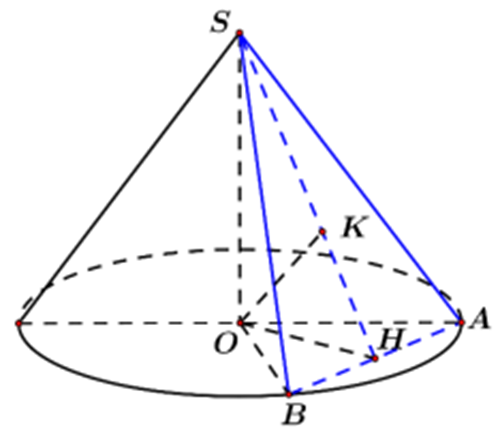
Cho hình nón đỉnh S có đường cao SO  a. Một mặt phẳng đi qua đỉnh của hình nón (ảnh 1)

Gọi H, K lần lượt là hình chiếu của O lên AB và SH.

Ta có: AB ^ (SOH) Þ AB ^ OK

Mà OK ^ SH nên OK ^ (SAB)

\( \Rightarrow OK = d\left( {O,\;\left( {SAB} \right)} \right) = \frac{{a\sqrt 2 }}{2}\)

Trong tam giác vuông SOH, ta có:

\(\frac{1}{{O{K^2}}} = \frac{1}{{O{S^2}}} + \frac{1}{{O{H^2}}} \Leftrightarrow \frac{1}{{O{H^2}}} = \frac{1}{{O{K^2}}} - \frac{1}{{O{S^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}}} - \frac{1}{{{a^2}}} = \frac{1}{{{a^2}}}\)

Þ OH = a

Khi đó: \(SH = \sqrt {S{O^2} + O{H^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)

Vì tam giác SAB vuông cân tại S nên có

\(SH = \frac{{AB}}{2} \Rightarrow AB = 2SH = 2a\sqrt 2 \)

Khi đó độ dài đường sinh là

l = SA = SB = 2a

Bán kính của đường tròn đáy là

\(r = OA = \sqrt {O{H^2} + H{A^2}} = \sqrt {{a^2} + {{\left( {\frac{{2a\sqrt 2 }}{2}} \right)}^2}} = a\sqrt 3 \)

Vậy diện tích xung quanh của hình nón là

\[{S_{xq}} = \pi \,.\,r\,.\,l = \pi \,.\,a\sqrt 3 .\,2a = 2\pi {a^2}\sqrt 3 \].

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Có bao nhiêu số gồm 5 chữ số phân biệt có mặt đủ ba chữ số 1,2,3.

Xem đáp án

Lời giải

Gọi số tự nhiên có 5 chữ số \(\overline {abcde} \;\left( {a \ne b \ne c \ne d \ne e;\;a \ne 0} \right)\)

+) Trường hợp với a là số bất kì kể cả 0

Xếp 3 số 1, 2, 3 vào 3 trong 5 vị trí và sắp xếp có \(A_5^3\) (cách)

Xếp 2 số trong 7 số còn lại vào 2 vị trí còn lại và sắp xếp có \(A_7^2\) (cách)

Suy ra có \(A_5^3\,.\,A_7^2\) số

+) Trường hợp a = 0

Chọn a có 1 cách

Xếp 3 số 1, 2, 3 vào 3 trong 4 vị trí và sắp xếp có \(A_4^3\) (cách)

Xếp 1 số còn lại trong 6 số vào 1 vị trí còn lại có \(C_6^1\) (cách)

Suy ra có \(A_4^3\,.\,C_7^1\) (cách)

Vậy có: \(A_5^3\,.\,A_7^2 - A_4^3\,.\,C_7^1 = 2376\) số thỏa mãn yêu cầu bài toán.

Câu 2

Trong mặt phẳng tọa độ Oxy, cho 3 điểm A(−4; 1), B(2; 4), C(2; −2).

a) Tìm tọa độ trọng tâm của tam giác ABC.

b) Tìm tọa độ điểm D sao cho C là trọng tâm của tam giác ABD.

c) Tìm tọa độ điểm E sao cho tứ giác ABCE là hình bình hành.

Xem đáp án

Lời giải

a) Gọi G là trọng tâm của tam giác ABC có tọa độ G(x_G; y_G).

Ta có: \(\left\{ \begin{array}{l}{x_G} = \frac{{ - 4 + 2 + 2}}{3} = 0\\{y_G} = \frac{{1 + 4 - 2}}{3} = 1\end{array} \right.\).

Vậy tọa độ trọng tâm G của tam giác ABC là G(0; 1).

b) Gỉả sử điểm D có tọa độ là D(x_D; y_D)

Vì C là trọng tâm của tam giác ABD nên ta có:

\(\left\{ \begin{array}{l}\frac{{ - 4 + 2 + {x_D}}}{3} = 2\\\frac{{1 + 4 + {y_D}}}{3} = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 4 + 2 + {x_D} = 6\\1 + 4 + {y_D} = - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 8\\{y_D} = - 11\end{array} \right.\)

Vậy điểm D có tọa độ là D(8; −11).

c) Gỉả sử điểm D có tọa độ là E(x_E; y_E).

Để tứ giác ABCE là hình bình hành thì \(\overrightarrow {AB} = \overrightarrow {EC} \)

\[ \Leftrightarrow \left( {2 + 4;\;4 - 1} \right) = \left( {2 - {x_E};\; - 2 - {y_E}} \right)\]

\( \Leftrightarrow \left\{ \begin{array}{l}2 - {x_E} = 6\\ - 2 - {y_E} = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_E} = - 4\\{y_E} = - 5\end{array} \right.\)

Vậy điểm E có tọa độ là E(−4; −5).

Câu 3