2. Lớp 11
  3. Toán

Câu hỏi:

13/07/2024 1,884

Một dao động điều hoà có phương trình li độ dao động là: x = Acos(ωt + φ), trong đó A, φ, ω là các hằng số (ω > 0). Khi đó, chu kì T của dao động là \(T = \frac{{2\pi }}{\omega }\).

Vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong mỗi trường hợp sau:

A = 3 và φ = 0;                A = 3 và \(\varphi = - \frac{\pi }{2}\);                 A = 3 và \(\varphi = \frac{\pi }{2}\).

Xem lời giải

Câu hỏi trong đề: Giải SGK Toán 11 Cánh Diều Hàm số lượng giác và đồ thị có đáp án !!

Bắt đầu thi Lưu câu hỏi

Quảng cáo

Trả lời:

verified
Giải bởi Vietjack

Từ \(T = \frac{{2\pi }}{\omega }\) ta có \(\omega = \frac{{2\pi }}{T}\).

Khi đó ta có phương trình li độ là \(x = A\cos \left( {\frac{{2\pi }}{T}.t + \varphi } \right)\).

* Với A = 3 và φ = 0 thay vào phương trình li độ \(x = A\cos \left( {\frac{{2\pi }}{T}.t + \varphi } \right)\) ta có:

\(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\).

• t = 0 thì x = 3cos0 = 3;

• \(t = \frac{T}{4}\) thì \(x = 3\cos \left( {\frac{{2\pi }}{T}.\frac{T}{4}} \right) = 3\cos \frac{\pi }{2} = 0\);

• \(t = \frac{T}{2}\) thì \(x = 3\cos \left( {\frac{{2\pi }}{T}.\frac{T}{2}} \right) = 3\cos \pi = - 3\)

• \(t = \frac{{3T}}{4}\) thì \(x = 3\cos \left( {\frac{{2\pi }}{T}.\frac{{3T}}{4}} \right) = 3\cos \frac{{3\pi }}{2} = 0\);

• t = T thì \(x = 3\cos \left( {\frac{{2\pi }}{T}.T} \right) = 3\cos 2\pi = 3\)  

‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà \(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; 2T]:

Xét hàm số \(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\) có chu kì là T.

Ta vẽ đồ thị hàm số \(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; T] theo bảng sau:

Vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong mỗi trường (ảnh 1)

Bằng cách dịch chuyển đồ thị hàm số \(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; T] song song với trục hoành sang phải theo đoạn có độ dài T, ta sẽ nhận được đồ thị hàm số \(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [T; 2T].

Từ đó ta vẽ được đồ thị biểu diễn li độ của dao động điều hoà \(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; 2T] như sau:

Vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong mỗi trường (ảnh 2)

* Với A = 3 và \(\varphi = - \frac{\pi }{2}\) thay vào phương trình li độ \(x = A\cos \left( {\frac{{2\pi }}{T}.t + \varphi } \right)\) ta có:

\(x = 3\cos \left( {\frac{{2\pi }}{T}.t - \frac{\pi }{2}} \right)\)\[ = 3\cos \left( {\frac{\pi }{2} - \frac{{2\pi }}{T}.t} \right) = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\]

• t = 0 thì \(x = 3\sin \left( {\frac{{2\pi }}{T}.0} \right) = 3\sin 0 = 0\)

• \(t = \frac{T}{4}\) thì \(x = 3\sin \left( {\frac{{2\pi }}{T}.\frac{T}{4}} \right) = 3\sin \frac{\pi }{2} = 3\);

• \(t = \frac{T}{2}\) thì \(x = 3\sin \left( {\frac{{2\pi }}{T}.\frac{T}{2}} \right) = 3\sin \pi = 0\);

• \(t = \frac{{3T}}{4}\) thì \[x = 3\sin \left( {\frac{{2\pi }}{T}.\frac{{3T}}{4}} \right) = 3\sin \frac{{3\pi }}{2} = - 3\];

• t = T thì \[x = 3\sin \left( {\frac{{2\pi }}{T}.T} \right) = 3\sin 2\pi = 0\].

‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; 2T]:

Xét hàm số \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) có chu kì là T.

Ta vẽ đồ thị hàm số \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; T] theo bảng sau:

Vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong mỗi trường (ảnh 3)

Bằng cách dịch chuyển đồ thị hàm số \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; T] song song với trục hoành sang phải theo đoạn có độ dài T, ta sẽ nhận được đồ thị hàm số \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [T; 2T].

Từ đó ta vẽ được đồ thị biểu diễn li độ của dao động điều hoà \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; 2T] như sau:

Vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong mỗi trường (ảnh 4)

* Với A = 3 và \(\varphi = \frac{\pi }{2}\) thay vào phương trình li độ \(x = A\cos \left( {\frac{{2\pi }}{T}.t + \varphi } \right)\) ta có:

\[x = 3\cos \left( {\frac{{2\pi }}{T}.t + \frac{\pi }{2}} \right) = - 3\cos \left[ {\pi - \left( {\frac{{2\pi }}{T}.t + \frac{\pi }{2}} \right)} \right]\]

    \( = - 3\cos \left( {\frac{\pi }{2} - \frac{{2\pi }}{T}.t} \right) = - 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\).

• t = 0 thì \(x = - 3\sin \left( {\frac{{2\pi }}{T}.0} \right) = - 3\sin 0 = 0\)

• \(t = \frac{T}{4}\) thì \[x = 3\sin \left( {\frac{{2\pi }}{T}.\frac{T}{4}} \right) = - 3\sin \frac{\pi }{2} = - 3\];              

• \(t = \frac{T}{2}\) thì \(x = - 3\sin \left( {\frac{{2\pi }}{T}.\frac{T}{2}} \right) = - 3\sin \pi = 0\);

• \(t = \frac{{3T}}{4}\) thì \[x = - 3\sin \left( {\frac{{2\pi }}{T}.\frac{{3T}}{4}} \right) = - 3\sin \frac{{3\pi }}{2} = 3\];

• t = T thì \[x = - 3\sin \left( {\frac{{2\pi }}{T}.T} \right) = - 3\sin 2\pi = 0\].

‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà \(x = - 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; 2T]:

Đồ thị hàm số \(x = - 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) là hình đối xứng với đồ thị hàm số \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) qua trục hoành:

Vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong mỗi trường (ảnh 5)

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:
Xem thêm »
  1. Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
  2. Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
  3. Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
  4. Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )

Bình luận


Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Xét tính chẵn, lẻ của các hàm số:

a) y = sinx cosx;

b) y = tanx + cotx;

c) y = sin2x.

Lời giải

a) Xét hàm số f(x) = y = sinx cosx có tập xác định D = ℝ:

• ∀x ∈ D thì ‒x ∈ D;

• f(‒x) = sin(‒x) . cos(‒x) = ‒sinx cosx = ‒f(x).

Do đó hàm số y = sinx cosx là hàm số lẻ.

b) Xét hàm số f(x) = y = tanx + cotx có tập xác định \(D = \mathbb{R}\backslash \left\{ {k\pi ;\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\):

• ∀x ∈ D thì ‒x ∈ D;

• f(‒x) = tan(‒x) + cot(‒x) = (‒tanx) + (‒cotx) = ‒(tanx + cotx) = ‒f(x).

Do đó hàm số y = tanx + cotx là hàm số lẻ.

c) Xét hàm số f(x) = y = sin2x có tập xác định D = ℝ:

• ∀x ∈ D thì ‒x ∈ D;

• f(‒x) = sin2(‒x) = (‒sinx)2 = sin2x = f(x).

Do đó hàm số y = sin2x là hàm số chẵn.

Câu 2

Quan sát đồ thị hàm số y = sinx ở Hình 24.

Tìm khoảng đồng biến, nghịch biến của hàm số y = sinx (ảnh 1)

Tìm khoảng đồng biến, nghịch biến của hàm số y = sinx.

Lời giải

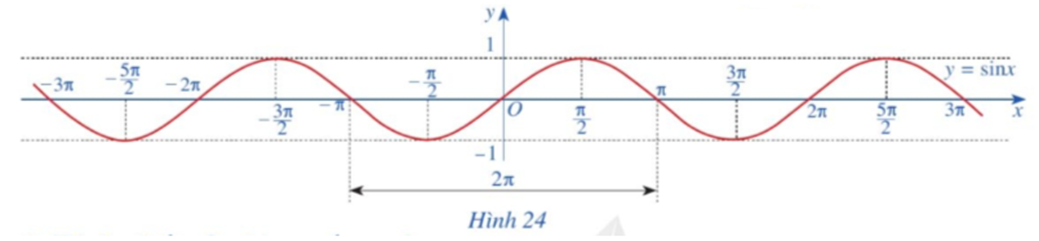
Quan sát đồ thị hàm số y = sinx ta thấy:

• Hàm số đồng biến trên mỗi khoảng \(\left( { - \frac{{5\pi }}{2}; - \frac{{3\pi }}{2}} \right);\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right);\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right);...\)

Ta có: \(\left( { - \frac{{5\pi }}{2}; - \frac{{3\pi }}{2}} \right) = \left( { - \frac{\pi }{2} - 2\pi ;\frac{\pi }{2} - 2\pi } \right)\);

            \[\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right) = \left( { - \frac{\pi }{2} + 2\pi ;\frac{\pi }{2} + 2\pi } \right)\];

             …

Do đó ta có thể viết hàm số đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) với k ∈ ℤ.

• Hàm số nghịch biến trên mỗi khoảng \(\left( { - \frac{{7\pi }}{2}; - \frac{{5\pi }}{2}} \right);\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right);\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right);...\)

Ta có: \[\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) = \left( {\frac{\pi }{2} - 2\pi ;\frac{{3\pi }}{2} - 2\pi } \right)\];

             …

Do đó ta có thể viết hàm số nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với k ∈ ℤ.

Câu 3

Quan sát đồ thị hàm số y = cotx ở Hình 31.

Tìm khoảng đồng biến, nghịch biến của hàm số y = cotx (ảnh 1)

Tìm khoảng đồng biến, nghịch biến của hàm số y = cotx.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Quan sát đồ thị hàm số y = cosx ở Hình 27.

Tìm khoảng đồng biến, nghịch biến của hàm số y = cosx (ảnh 1)

Tìm khoảng đồng biến, nghịch biến của hàm số y = cosx.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

y = sinx trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right),\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\);

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Guồng nước (hay còn gọi là cọn nước) không chỉ là công cụ phục vụ sản xuất nông nghiệp, mà đã trở thành hình ảnh quen thuộc của bản làng và là một nét văn hoá đặc trưng của đồng bào dân tộc miền núi phía Bắc.

Guồng nước (hay còn gọi là cọn nước) không chỉ là công cụ phục vụ sản xuất nông (ảnh 1)

Một chiếc guồng nước có dạng hình tròn bán kính 2,5 m; trục của nó đặt cách mặt nước 2 m. Khi guồng quay đều, khoảng cách h (m) từ một ống đựng nước gắn tại một điểm của guồng đến mặt nước được tính theo công thức h = |y|, trong đó \(y = 2,5\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2\), với x (phút) là thời gian quay của guồng (x ≥ 0).

(Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020).

Khoảng cách h phụ thuộc vào thời gian quay x như thế nào?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:

Hàm số y = sinx nhận giá trị bằng 1;

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »
Hỏi bài tập
Vietjack official store
Đăng ký gói thi VIP

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

  • Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

  • Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

  • Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

  • Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

🔥 Đề thi HOT:

  1. 1856 người thi tuần này

    10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
  2. 521 người thi tuần này

    Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
  3. 294 người thi tuần này

    Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
  4. 196 người thi tuần này

    38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
  5. 189 người thi tuần này

    12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
  6. 186 người thi tuần này

    15 câu Trắc nghiệm Khoảng cách có đáp án (Nhận biết)
  7. 181 người thi tuần này

    Bài tập Tổ hợp - Xác suất cơ bản, nâng cao có lời giải chi tiết (P6)
  8. 165 người thi tuần này

    10 Bài tập Biến cố hợp. Biến cố giao (có lời giải)

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.

Đăng ký

Bạn đã có tài khoản?