Một miếng bìa có dạng hình vuông với độ dài cạnh là x (cm). Người ta cắt đi ở mỗi góc của miếng bìa một hình vuông sao cho bốn hình vuông bị cắt đi có cùng độ dài cạnh là y (cm) với 0 < 2y < x (Hình 2).

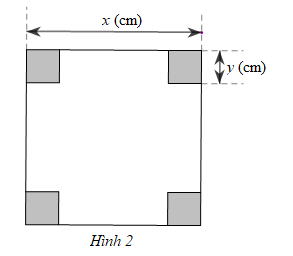
a) Viết phân thức biểu thị tỉ số diện tích của miếng bìa ban đầu và phần miếng bìa còn lại sau khi bị cắt.

b) Tính giá trị của phân thức đó tại x = 4; y = 1.

Lời giải

a) Ta có: 15x³y² = 5x³y².3; 10x⁴z³ = 5x³.2xz³; 20y³z = 5y³z.4.

Chọn MTC là: 60x⁴y³z³

Nhân tử phụ của ba mẫu thức 15x³y²; 10x⁴z³; 20y³z lần lượt là: 4xyz³; 6y³; 3x⁴z².

Vậy: \(\frac{2}{{15{x^3}{y^2}}} = \frac{{2.4xy{z^3}}}{{15{x^3}{y^2}.4xy{z^3}}} = \frac{{8xy{z^3}}}{{60{x^4}{y^3}{z^3}}}\)

\(\frac{y}{{10{x^4}{z^3}}} = \frac{{y.6{y^3}}}{{10{x^4}{z^3}.6{y^3}}} = \frac{{6{y^4}}}{{60{x^4}{y^3}{z^3}}}\)

\(\frac{x}{{20{y^3}z}} = \frac{{x.3{x^4}{z^2}}}{{20{y^3}z.3{x^4}{z^2}}} = \frac{{3{x^5}{z^2}}}{{60{x^4}{y^3}{z^3}}}\).

b) Ta có: 2x + 6 = 2(x + 3); x² ‒ 9 = (x ‒ 3)(x + 3)

Chọn MTC là: 2(x ‒ 3)(x + 3).

Nhân tử phụ của hai mẫu thức 2x + 6 và x² ‒ 9 lần lượt là: (x ‒ 3) và 2

Vậy: \(\frac{x}{{2x + 6}} = \frac{{x\left( {x - 3} \right)}}{{2\left( {x + 3} \right)\left( {x - 3} \right)}} = \frac{{x\left( {x - 3} \right)}}{{2\left( {{x^2} - 9} \right)}}\);

          \(\frac{4}{{{x^2} - 9}} = \frac{{4.2}}{{2\left( {{x^2} - 9} \right)}} = \frac{8}{{2\left( {{x^2} - 9} \right)}}\).

c) Ta có: x³ ‒ 1 = (x ‒ 1)(x² + x + 1) và x² + x + 1 = x² + x + 1

Chọn MTC là: x³ ‒ 1 = (x ‒ 1)(x² + x + 1)

Nhân tử phụ của hai mẫu thức x³ ‒ 1 và x² + x + 1 lần lượt là: 1 và x ‒ 1.

Vậy: \(\frac{{2x}}{{{x^3} - 1}} = \frac{{2x}}{{{x^3} - 1}}\) và \(\frac{{x - 1}}{{{x^2} + x + 1}} = \frac{{\left( {x - 1} \right)\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} = \frac{{{{\left( {x - 1} \right)}^2}}}{{{x^3} - 1}}\).

d) Ta có: 1 + 2x + x² = (1 + x)²;

               5x² ‒ 5 = 5(x² ‒ 1) = 5(x ‒ 1)(x + 1).

Chọn MTC là: 5(x ‒ 1)(x + 1)²

Nhân tử phụ của hai mẫu thức 1 + 2x + x² và 5x² ‒ 5 lần lượt là: 5(x ‒ 1) và x + 1.

Vậy: \(\frac{x}{{1 + 2x + {x^2}}} = \frac{{x.5.\left( {x - 1} \right)}}{{\left( {1 + 2x + {x^2}} \right).5.\left( {x - 1} \right)}} = \frac{{5x\left( {x - 1} \right)}}{{5\left( {x - 1} \right){{\left( {x + 1} \right)}^2}}}\)

\(\frac{3}{{5{x^2} - 5}} = \frac{{3.\left( {x + 1} \right)}}{{5\left( {x - 1} \right)\left( {x + 1} \right)\left( {x + 1} \right)}} = \frac{{3\left( {x + 1} \right)}}{{5\left( {x - 1} \right){{\left( {x + 1} \right)}^2}}}\).

Lời giải

a) Ta có: x²y³.2 = 2x²y³ và 2x²y².y = 2x²y³ nên x²y³.2 = 2x²y².y

Vậy \(\frac{{{x^2}{y^3}}}{{2{x^2}{y^2}}} = \frac{y}{2}\).

b) Ta có:

(x² ‒ x ‒ 2).(x ‒ 1) = x³ ‒ x² ‒ x² + x ‒ 2x + 2 = x³ ‒ 2x² ‒ x + 2

Và (x² ‒ 3x + 2)(x + 1) = x³ + x² ‒ 3x² ‒ 3x + 2x + 2 =  x³ ‒ 2x² ‒ x + 2

Nên (x² ‒ x ‒ 2).(x ‒ 1) = (x² ‒ 3x + 2)(x + 1)

Vậy \(\frac{{{x^2} - x - 2}}{{x + 1}} = \frac{{{x^2} - 3x + 2}}{{x - 1}}\).

c) Ta có:

(x + 3)(x² ‒ 3x + 9) = x³ + 3³ = x³ + 27

Và (x³ + 27).1 = x³ + 27

Nên (x² ‒ 3x + 9)(x + 3) = (x³ + 27).1

Vậy \(\frac{{{x^2} - 3x + 9}}{{{x^3} + 27}} = \frac{1}{{x + 3}}\).