Câu hỏi:
13/07/2024 467
Hai máy bay cùng bay quãng đường 600 km. Biết tốc độ của máy bay thứ hai lớn hơn tốc độ của máy bay thứ nhất là 300 km/h. Gọi x km/h là tốc độ của máy bay thứ nhất (x > 0). Viết phân thức biểu thị theo x:
a) Thời gian máy bay thứ nhất đã bay;
b) Thời gian máy bay thứ hai đã bay;
c) Tỉ số của thời gian máy bay thứ nhất đã bay và thời gian máy bay thứ hai đã bay.
Hai máy bay cùng bay quãng đường 600 km. Biết tốc độ của máy bay thứ hai lớn hơn tốc độ của máy bay thứ nhất là 300 km/h. Gọi x km/h là tốc độ của máy bay thứ nhất (x > 0). Viết phân thức biểu thị theo x:
a) Thời gian máy bay thứ nhất đã bay;
b) Thời gian máy bay thứ hai đã bay;
c) Tỉ số của thời gian máy bay thứ nhất đã bay và thời gian máy bay thứ hai đã bay.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
a) Phân thức biểu thị thời gian máy bay thứ nhất đã bay là: \(\frac{{600}}{x}\) (giờ).
b) Phân thức biểu thị thời gian máy bay thứ hai đã bay là: \(\frac{{600}}{{x + 300}}\) (giờ).
c) Tỉ số của thời gian máy bay thứ nhất đã bay và thời gian máy bay thứ hai đã bay là:
\(\frac{{600}}{x}:\frac{{600}}{{x + 300}} = \frac{{600}}{x} \cdot \frac{{x + 300}}{{600}} = \frac{{x + 300}}{x}\)
Vậy phân thức biểu thị tỉ số của thời gian máy bay thứ nhất đã bay và thời gian máy bay thứ hai đã bay là: \(\frac{{x + 300}}{x}\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
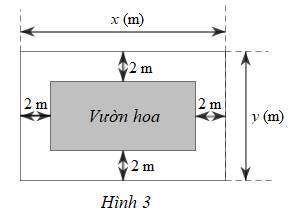
Chiều dài của vườn hoa là: x ‒ 2 ‒ 2 = x ‒ 4 (m).
Chiều rộng của vườn hoa là: y ‒ 2 ‒ 2 = y ‒ 4(m).
a) Diện tích của mảnh đất là: xy (m2).
Diện tích của vườn hoa là: (x ‒ 4)(y ‒ 4) = xy ‒ 4x ‒ 4y + 16 (m2).
Phân thức biểu thị tỉ số diện tích của mảnh đất và vườn hoa là:
\(\frac{{xy}}{{xy - 4x - 4y + 16}}\).
b) Chu vi của mảnh đất là: 2(x + y) (m).
Chu vi của vườn hoa là: 2(x ‒ 4 + y ‒ 4) = 2(x + y ‒ 8) (m).
Phân thức biểu thị tỉ số chu vi của mảnh đất và vườn hoa là:
\(\frac{{2\left( {x + y} \right)}}{{2\left( {x + y - 8} \right)}} = \frac{{x + y}}{{x + y - 8}}\).
Lời giải
Lời giải
a) Ta có: \(M = \frac{{x - 2y}}{{3x + 6y}}:\frac{{{x^2} - 4{y^2}}}{{{x^2} + 4xy + 4{y^2}}}\)
\( = \frac{{x - 2y}}{{3x + 6y}}.\frac{{{x^2} + 4xy + 4{y^2}}}{{{x^2} - 4{y^2}}}\)
\( = \frac{{\left( {x - 2y} \right)\left( {{x^2} + 4xy + 4{y^2}} \right)}}{{\left( {3x + 6y} \right)\left( {{x^2} - 4{y^2}} \right)}}\)
\( = \frac{{\left( {x - 2y} \right){{\left( {x + 2y} \right)}^2}}}{{3.\left( {x + 2y} \right)\left( {x + 2y} \right)\left( {x - 2y} \right)}} = \frac{1}{3}\).
Vậy giá trị của M không phụ thuộc vào giá trị của biến.
b) \(N = \left( {x - \frac{{{x^2} + {y^2}}}{{x + y}}} \right)\left( {\frac{1}{y} + \frac{2}{{x - y}}} \right)\)
\( = \left[ {\frac{{x\left( {x + y} \right)}}{{x + y}} - \frac{{{x^2} + {y^2}}}{{x + y}}} \right].\left[ {\frac{{x - y}}{{y\left( {x - y} \right)}} + \frac{{2y}}{{y\left( {x - y} \right)}}} \right]\)
\( = \frac{{{x^2} + xy - {x^2} - {y^2}}}{{x + y}}.\frac{{x - y + 2y}}{{y\left( {x - y} \right)}}\)
\( = \frac{{xy - {y^2}}}{{x + y}}.\frac{{x + y}}{{y\left( {x - y} \right)}}\)
\( = \frac{{y\left( {x - y} \right)\left( {x + y} \right)}}{{y\left( {x + y} \right)\left( {x - y} \right)}} = 1\).
Vậy giá trị của N không phụ thuộc vào giá trị của biến.
c) \(P = \left( {\frac{{{x^3} + {y^3}}}{{x + y}} - xy} \right):\left( {{x^2} - {y^2}} \right) + \frac{{2y}}{{x + y}}\)
\( = \left[ {\frac{{{x^3} + {y^3}}}{{x + y}} - \frac{{xy\left( {x + y} \right)}}{{x + y}}} \right].\frac{1}{{{x^2} - {y^2}}} + \frac{{2y}}{{x + y}}\)
\( = \frac{{\left( {x + y} \right)\left( {{x^2} - xy + {y^2}} \right) - xy\left( {x + y} \right)}}{{x + y}}.\frac{1}{{{x^2} - {y^2}}} + \frac{{2y}}{{x + y}}\)
\( = \frac{{\left( {x + y} \right)\left( {{x^2} - xy + {y^2} - xy} \right)}}{{x + y}}.\frac{1}{{\left( {x - y} \right)\left( {x + y} \right)}} + \frac{{2y}}{{x + y}}\)
\( = \frac{{{{\left( {x - y} \right)}^2}}}{{\left( {x - y} \right)\left( {x + y} \right)}} + \frac{{2y}}{{x + y}}\)
\( = \frac{{x - y}}{{x + y}} + \frac{{2y}}{{x + y}} = \frac{{x + y}}{{x + y}} = 1\).
Vậy giá trị của P không phụ thuộc vào giá trị của biến.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 4