Câu hỏi:
13/07/2024 3,209
Hiện tại, cô Hạnh đã tiết kiệm được 500 triệu đồng. Để thực hiện dự định mua một căn chung cư có giá trị 2,6 tỉ đồng, cô Hạnh đã lên kế hoạch hằng tháng tiết kiệm 15 triệu đồng. Gọi y (triệu đồng) là số tiền cô Hạnh tiết kiệm được sau x (tháng) kể từ hiện tại.
a) Viết công thức tính y theo x. Hỏi y có phải là hàm số bậc nhất của x hay không?
b) Hỏi sau bao lâu kể từ hiện tại thì cô Hạnh có thể mua được căn hộ chung cư đó bằng tiền tiết kiệm?
Hiện tại, cô Hạnh đã tiết kiệm được 500 triệu đồng. Để thực hiện dự định mua một căn chung cư có giá trị 2,6 tỉ đồng, cô Hạnh đã lên kế hoạch hằng tháng tiết kiệm 15 triệu đồng. Gọi y (triệu đồng) là số tiền cô Hạnh tiết kiệm được sau x (tháng) kể từ hiện tại.
a) Viết công thức tính y theo x. Hỏi y có phải là hàm số bậc nhất của x hay không?
b) Hỏi sau bao lâu kể từ hiện tại thì cô Hạnh có thể mua được căn hộ chung cư đó bằng tiền tiết kiệm?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
a) Công thức tính y theo x là: y = 15x + 500. Vậy y là hàm số bậc nhất của x.
b) Đổi 2,6 tỉ đồng = 2 600 triệu đồng.
Để cô Hạnh mua đuộc căn hộ chung cư đó thì số tiền tiết kiệm được là 2 600 đồng.
Do đó 15x + 500 = 2600
Suy ra = 140.
Mà 140 tháng = 11 năm + 8 tháng, nên sau 11 năm 8 tháng kể từ hiện tại thì cô Hạnh có thể mua được căn hộ chung cư đó bằng tiền tiết kiệm.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
a) Do đường thẳng d: y = ax + b (a ≠ 0) song song với đường thẳng \(d':y = - 3x - \frac{2}{3}\) nên a = ‒3 (thoả mãn) và \(b \ne - \frac{2}{3}\).
Mà đường thẳng y = ax + b đi qua điểm A(‒2; ‒4) suy ra ‒4 = ‒3.(‒2) + b hay b = ‒10 (thoả mãn).
Do đó, đường thẳng cần tìm là y = ‒3x ‒ 10.
b) Đường thẳng d có hệ số góc bằng ‒3 nên y = ‒3x + b.
Với y = 0 vào y = 2x – 2 ta được 2x – 2 = 0, suy ra x = 1.
Do đó B là giao điểm của đường thẳng y = 2x – 2 với trục hoành nên B(1; 0).
Do đường thẳng d đi qua điểm B(1; 0) nên thay x = 1, y = 0 vào y = ‒3x + b ta có:
0 = ‒3.1 + b
Suy ra b = 3
Từ đó, ta tìm được d: y = –3x + 3.
Lời giải
Lời giải
a) Ta có: A(‒2; 0), B(0; 4).
b) Ta vẽ các điểm M, N lần lượt là trung điểm của OA, OB như hình vẽ:
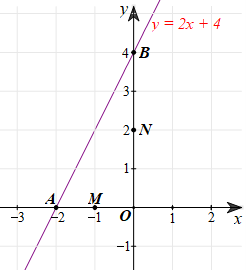
Từ đó ta có: M(‒1; 0), N(0; 2).
c) Do A, B lần lượt nằm trên Ox, Oy nên tam giác OAB vuông tại O.
Do đó diện tích của tam giác OAB là: \({S_{\Delta OAB}} = \frac{1}{2} \cdot OA \cdot OB\).
Mà M, N lần lượt là trung điểm của OA, OB nên \(OM = \frac{1}{2}OA,ON = \frac{1}{2}OB\).
Do M, N lần lượt nằm trên Ox, Oy nên tam giác OMN vuông tại O nên ta có diện tích của tam giác OMN bằng:
\({S_{\Delta OMN}} = \frac{1}{2} \cdot OM \cdot ON = \frac{1}{2} \cdot \frac{1}{2}OA \cdot \frac{1}{2}OB = \frac{1}{4} \cdot \frac{1}{2} \cdot OA.OB = \frac{1}{4}{S_{\Delta OAB}}\)
Vậy tỉ số phần trăm của diện tích tam giác \(OMN\) và diện tích tam giác \(OAB\) là:
\(\frac{{\frac{1}{4}{S_{\Delta OAB}}}}{{{S_{\Delta OAB}}}}.100\% = 25\% \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
10 Bài tập Nhận biết đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn thức (có lời giải)
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
-
Dạng 8: Bài luyện tập 3 dạng 4. Tổng hợp có đáp án
-
Dạng 2: Bài luyện tập 1 Dạng 2: Rút gọn phân thức có đáp án