Câu hỏi:
13/07/2024 3,158
Trong mặt phẳng toạ độ Oxy, cho các điểm A(2; 3), B(2 ; ‒4). Tìm toạ độ điểm C sao cho C nằm trên trục Ox và CA + CB đạt giá trị nhỏ nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
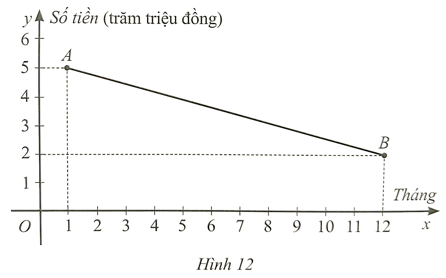
Biểu diễn điểm A(2; 3), B(2 ; ‒4) trên mặt phẳng tọa độ Oxy như hình vẽ sau:
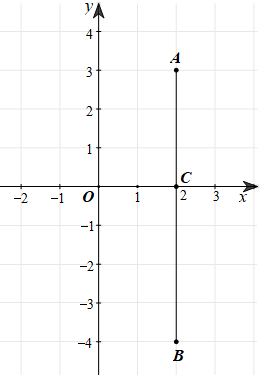
Khi C nằm trên trục Ox thì có 2 trường hợp xảy ra:
• Trường hợp 1: Ba điểm A, B, C không thẳng hàng, khi đó tạo thành tam giác ABC.
Theo bất đẳng thức tam giác ta có: CA + CB > AB.
• Trường hợp 2: Ba điểm A, B, C thẳng hàng, khi đó CA + CB = AB.
Từ 2 trường hợp trên ta được: CA + CB ≥ AB
Do đó CA + CB đạt giá trị nhỏ nhất bằng AB, khi ba điểm A, B, C thẳng hàng.
Khi đó, C là giao điểm của AB và trục Ox.
Vậy C(2; 0).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
a) Do đường thẳng d: y = ax + b (a ≠ 0) song song với đường thẳng \(d':y = - 3x - \frac{2}{3}\) nên a = ‒3 (thoả mãn) và \(b \ne - \frac{2}{3}\).
Mà đường thẳng y = ax + b đi qua điểm A(‒2; ‒4) suy ra ‒4 = ‒3.(‒2) + b hay b = ‒10 (thoả mãn).
Do đó, đường thẳng cần tìm là y = ‒3x ‒ 10.
b) Đường thẳng d có hệ số góc bằng ‒3 nên y = ‒3x + b.
Với y = 0 vào y = 2x – 2 ta được 2x – 2 = 0, suy ra x = 1.
Do đó B là giao điểm của đường thẳng y = 2x – 2 với trục hoành nên B(1; 0).
Do đường thẳng d đi qua điểm B(1; 0) nên thay x = 1, y = 0 vào y = ‒3x + b ta có:
0 = ‒3.1 + b
Suy ra b = 3
Từ đó, ta tìm được d: y = –3x + 3.
Lời giải
Lời giải
a) Ta có: A(‒2; 0), B(0; 4).
b) Ta vẽ các điểm M, N lần lượt là trung điểm của OA, OB như hình vẽ:
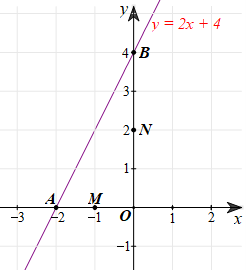
Từ đó ta có: M(‒1; 0), N(0; 2).
c) Do A, B lần lượt nằm trên Ox, Oy nên tam giác OAB vuông tại O.
Do đó diện tích của tam giác OAB là: \({S_{\Delta OAB}} = \frac{1}{2} \cdot OA \cdot OB\).
Mà M, N lần lượt là trung điểm của OA, OB nên \(OM = \frac{1}{2}OA,ON = \frac{1}{2}OB\).
Do M, N lần lượt nằm trên Ox, Oy nên tam giác OMN vuông tại O nên ta có diện tích của tam giác OMN bằng:
\({S_{\Delta OMN}} = \frac{1}{2} \cdot OM \cdot ON = \frac{1}{2} \cdot \frac{1}{2}OA \cdot \frac{1}{2}OB = \frac{1}{4} \cdot \frac{1}{2} \cdot OA.OB = \frac{1}{4}{S_{\Delta OAB}}\)
Vậy tỉ số phần trăm của diện tích tam giác \(OMN\) và diện tích tam giác \(OAB\) là:
\(\frac{{\frac{1}{4}{S_{\Delta OAB}}}}{{{S_{\Delta OAB}}}}.100\% = 25\% \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo