Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Với mọi n ∈ ℕ* ta có
(luôn đúng)
Áp dụng bất đẳng thức trên ta có
...
Suy ra
Vậy .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
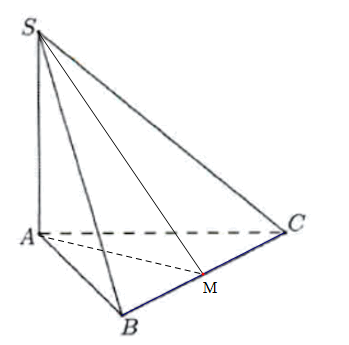
Gọi M là trung điểm của BC
Suy ra AM là trung tuyến của tam giác ABC
Do đó
Mà tam giác ABC đều nên AM ⊥ BC
Mà SA ⊥ BC nên BC ⊥ (SAM)
Suy ra (SBC) ⊥ (SAM)
Ta có SA ⊥ (ABC)
Suy ra (SAM) ⊥ (ABC)
Do đó góc giữa (SBC) và (ABC) là
Xét tam giác SAM vuông tại A có
Nên tam giác SAM vuông cân tại A
Suy ra
Ta có: .
Vậy ta chọn đáp án A.
Lời giải
Điều kiện x > 0
Áp dụng công thức đổi cơ số, ta có:
Ta có:
Do đó từ phương trình trên, ta phải có log2x = 0 hay x = 20 = 1
Vậy phương trình có nghiệm duy nhất x = 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. m < 1;
B. m ≤ 0;
C. m < 0;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.