Hình 4 mô tả một chiếc thước của người thợ sử dụng khi xây móng nhà để kiểm tra xem hai phần móng nhà có vuông góc với nhau hay không. Trên hình, ta đo được AB = 4 dm, AC = 3 dm và BC = 5 dm. Em hãy giải thích vì sao hai cạnh của chiếc thước đó vuông góc với nhau.
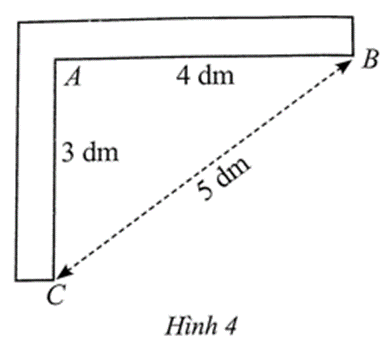
Hình 4 mô tả một chiếc thước của người thợ sử dụng khi xây móng nhà để kiểm tra xem hai phần móng nhà có vuông góc với nhau hay không. Trên hình, ta đo được AB = 4 dm, AC = 3 dm và BC = 5 dm. Em hãy giải thích vì sao hai cạnh của chiếc thước đó vuông góc với nhau.

Câu hỏi trong đề: Giải SBT Toán 8 Cánh Diều Định lí Pythagore có đáp án !!
Quảng cáo
Trả lời:
Ta có: 52 = 25; 42 + 32 = 16 + 9 = 25 nên 52 = 42 + 32.
Do đó, tam giác ABC vuông tại A (theo định lí Pythagore đảo).
Vậy hai cạnh của chiếc thước đó vuông góc với nhau.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
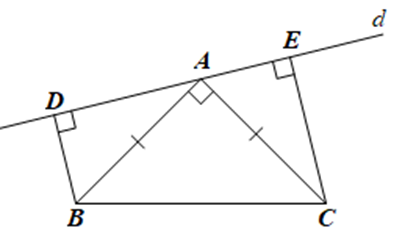
Do BD ⊥ d nên \(\widehat {ADB} = 90^\circ \), do đó tam giác ABD vuông tại D
Suy ra \(\widehat {ABD} + \widehat {BAD} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°) (1)
Mà \[\widehat {BAD} + \widehat {BAC} + \widehat {CAE} = 180^\circ \]
Suy ra \[\widehat {BAD} + \widehat {CAE} = 180^\circ - \widehat {BAC} = 180^\circ - 90^\circ = 90^\circ \] (2)
Từ (1) và (2) ta có \(\widehat {ABD} = \widehat {CAE}\).
Xét ∆ABD vuông tại D và ∆CAE vuông tại E có:
AB = CA, \(\widehat {ABD} = \widehat {CAE}\)
Do đó ∆ABD = ∆CAE (cạnh huyền – góc nhọn)
Suy ra AD = CE (hai cạnh tương ứng)
Khi đó AD2 + AE2 = CE2 + AE2 = AC2 (do tam giác CAE vuông tại E)
Vậy AD2 + AE2 không phụ thuộc vào vị trí của đường thẳng d.
Lời giải
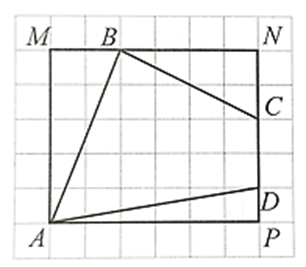
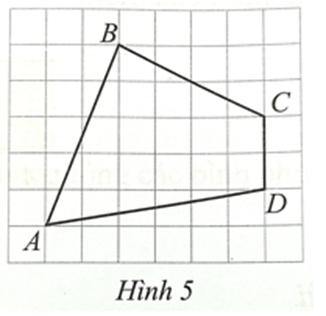
Vẽ các điểm M, N, P như hình vẽ.
Do tam giác ABM vuông tại M nên theo định lý Pythagore, ta có:
AB2 = MB2 + MA2 = 22 + 52 = 4 + 25 = 29
Suy ra \[AB = \sqrt {29} \;\;\left( {{\rm{cm}}} \right)\]
Tương tự, ta có:
• BC2 = NB2 + NC2 = 42 + 22 = 16 + 4 = 20. Suy ra \[BC = \sqrt {20} \;\;\left( {{\rm{cm}}} \right)\].
• AD2 = AP2 + DP2 = 62 + 12 = 36 + 1 = 37. Suy ra \[AD = \sqrt {37} \;\;\left( {{\rm{cm}}} \right)\].
Vậy chu vi tứ giác ABCD là:
\[AB + BC + CD + AD = \sqrt {29} + \sqrt {20} + 2 + \sqrt {37} \approx 17,94\;\;\left( {{\rm{cm}}} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.