Câu hỏi:
13/07/2024 2,323
Cho tam giác ABC vuông cân tại A có độ dài cạnh góc vuông AB và AC là 4 cm. Kẻ đường cao AD của tam giác ABC.
Tính độ dài cạnh đáy BC (làm tròn kết quả đến hàng phần trăm của centimét).
Cho tam giác ABC vuông cân tại A có độ dài cạnh góc vuông AB và AC là 4 cm. Kẻ đường cao AD của tam giác ABC.
Tính độ dài cạnh đáy BC (làm tròn kết quả đến hàng phần trăm của centimét).Câu hỏi trong đề: Giải SBT Toán 8 Cánh Diều Định lí Pythagore có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
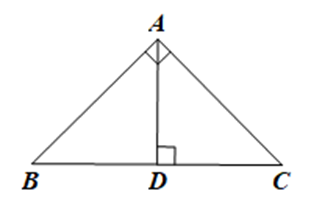
Do tam giác ABC vuông cân tại A nên theo định lý Pythagore ta có:
BC2 = AB2 + AC2 = 42 + 42 = 16 + 16 = 32
Suy ra \[BC = \sqrt {32} \approx 5,66\;\;\left( {{\rm{cm}}} \right)\].
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
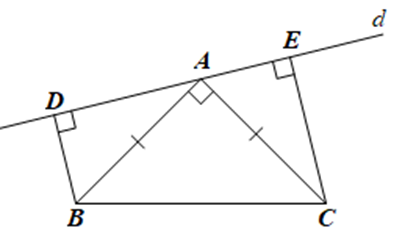
Do BD ⊥ d nên \(\widehat {ADB} = 90^\circ \), do đó tam giác ABD vuông tại D
Suy ra \(\widehat {ABD} + \widehat {BAD} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°) (1)
Mà \[\widehat {BAD} + \widehat {BAC} + \widehat {CAE} = 180^\circ \]
Suy ra \[\widehat {BAD} + \widehat {CAE} = 180^\circ - \widehat {BAC} = 180^\circ - 90^\circ = 90^\circ \] (2)
Từ (1) và (2) ta có \(\widehat {ABD} = \widehat {CAE}\).
Xét ∆ABD vuông tại D và ∆CAE vuông tại E có:
AB = CA, \(\widehat {ABD} = \widehat {CAE}\)
Do đó ∆ABD = ∆CAE (cạnh huyền – góc nhọn)
Suy ra AD = CE (hai cạnh tương ứng)
Khi đó AD2 + AE2 = CE2 + AE2 = AC2 (do tam giác CAE vuông tại E)
Vậy AD2 + AE2 không phụ thuộc vào vị trí của đường thẳng d.
Lời giải
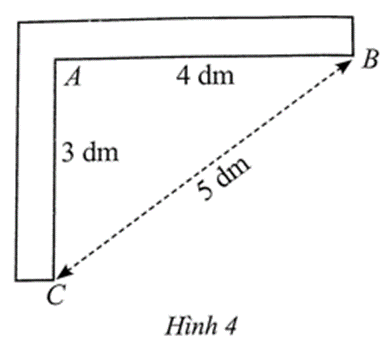
Ta có: 52 = 25; 42 + 32 = 16 + 9 = 25 nên 52 = 42 + 32.
Do đó, tam giác ABC vuông tại A (theo định lí Pythagore đảo).
Vậy hai cạnh của chiếc thước đó vuông góc với nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo