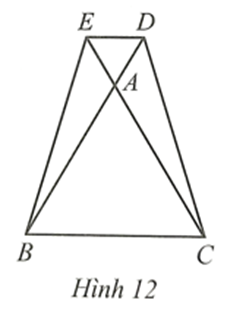
Cho tam giác ABC cân tại A. Lấy điểm M, N lần lượt trên cạnh AB, AC sao cho AM = AN.
Chứng minh tứ giác BMNC là hình thang cân.
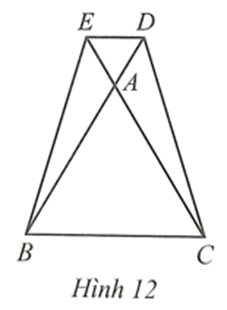
Cho tam giác ABC cân tại A. Lấy điểm M, N lần lượt trên cạnh AB, AC sao cho AM = AN.
Chứng minh tứ giác BMNC là hình thang cân.
Câu hỏi trong đề: Giải SBT Toán 8 Cánh Diều Hình thang cân có đáp án !!
Quảng cáo
Trả lời:
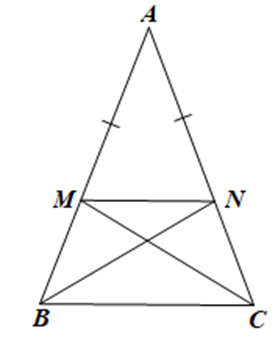
Do AM = AN nên ∆AMN cân tại A.
Xét ∆AMN cân tại A có: \[\widehat {AMN} = \widehat {ANM} = \frac{{180^\circ - \widehat A}}{2}\].
Xét ∆ABC đều hay cũng cân tại A có \[\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ - \widehat A}}{2}\].
Suy ra \[\widehat {AMN} = \widehat {ABC}\,\,\left( { = \frac{{180^\circ - \widehat A}}{2}} \right)\]
Mà \(\widehat {AMN}\) và \(\widehat {ABC}\) nằm ở vị trí đồng vị, suy ra MN // BC.
Tứ giác BMNC có MN // BC và \(\widehat {MBC} = \widehat {NCB}\) nên BMNC là hình thang cân.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
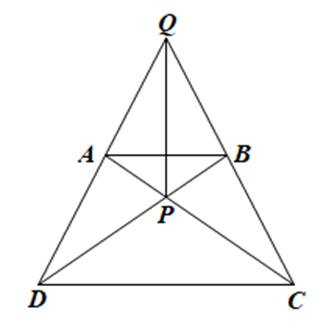
• Xét ∆ACD và ∆BDC có:
AD = BC;
\(\widehat {ADC} = \widehat {BCD}\) (do ABCD là hình thang cân);
CD là cạnh chung
Do đó ∆ACD = ∆BDC (c.g.c).
Suy ra \(\widehat {ACD} = \widehat {BDC}\) (hai góc tương ứng)
Tam giác PCD có \(\widehat {PCD} = \widehat {PDC}\) nên là tam giác cân tại P.
Suy ra PC = PD.
Mà AC = BD (do ∆ACD = ∆BDC);
AC = AP + PC; BD = PD + BD
Suy ra PA = PB nên P nằm trên đường trung trực của AB (1)
• Do AB // CD nên \(\widehat {QAB} = \widehat {ADC};\widehat {QBA} = \widehat {BCD}\) (các cặp góc đồng vị).
Mặt khác, \(\widehat {ADC} = \widehat {BCD}\) (do ∆ACD = ∆BDC) nên \(\widehat {QAB} = \widehat {QBA}\).
Do đó, tam giác QAB cân tại Q.
Suy ra QA = QB nên Q nằm trên đường trung trực của AB (2)
Từ (1) và (2) suy ra PQ là đường trung trực của AB.
• Ta có: AD = BC và PA = PB suy ra QD = QC.
Do đó Q nằm trên đường trung trực của CD.
Mặt khác PC = PD (chứng minh trên) nên P cũng nằm trên đường trung trực của CD.
Suy ra PQ là đường trung trực của CD.
Vậy PQ là đường trung trực của cả hai đoạn AB và CD.
Lời giải
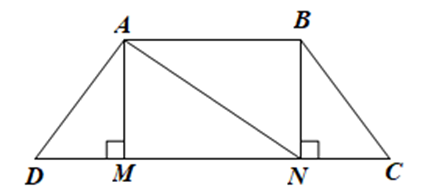
• Xét ∆ADM vuông tại M và ∆BCN vuông tại N có:
AD = BC; \(\widehat {ADM} = \widehat {BCN}\) (do ABCD là hình thang cân)
Do đó ∆ADM = ∆BCN (cạnh huyền – góc nhọn).
Suy ra AM = BN; DM = CN (các cặp cạnh tương ứng)
• Do AB // CD mà BN ⊥ CD nên BN ⊥ AB, do đó tam giác ABN vuông tại B.
Xét ∆ABN vuông tại B và ∆NMA vuông tại M có:
\(\widehat {BAN} = \widehat {MNA}\) (2 góc so le trong của AB // CD);
Cạnh AN chung
Do đó ∆ABN = ∆NMA (cạnh huyền – góc nhọn).
Suy ra AB = NM (hai cạnh tương ứng)
Mà AB = 3 cm nên NM = 3 cm.
• Ta có DM + NM + CN = CD và DM = CN nên 2DM + 3 = 6.
Suy ra DM = 1,5 cm.
Mà DN = DM + NM = 1,5 + 3 = 4,5 cm.
Trong tam giác ADM vuông tại M, ta có: AD2 = AM2 + DM2.
Suy ra AM2 = AD2 ‒ DM2 = 2,52 ‒ 1,52 = 4.
Vậy \(AM = \sqrt 4 = 2\;\;\left( {{\rm{cm}}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.