Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:

Đại đa số thanh niên thời trước không ai suy nghĩ, trăn trở gì lắm về cuộc đời, vì ai đã có phận nấy.

Phận là cái phận mà cuộc sống, xã hội dành cho mỗi người. Phận làm trai, phận giàu, phận nghèo, phận đàn bà, phận làm tôi,... Con nhà lao động nghèo, nhiều lắm học đến chín, mười tuổi, là đã phải lo làm ăn mong kế nghiệp cha, anh. Con nhà giàu theo học lên cao thì làm quan, kém hơn thì làm thầy. Sinh ra nó ở phận nào, theo phận ấy, chỉ số ít là thoát khỏi.

Trái lại, thanh niên ngày nay tuy cái phận mỗi người vẫn còn, song trước mặt mọi người đều có khả năng mở ra nhiều con đường. Ngày nay sự lựa chọn và cố gắng của bản thân, sự giúp đỡ của bạn bè đóng vai trò quyết định. Có lựa chọn tất phải có suy nghĩ, trăn trở.

Hết lớp tám, lớp chín, học gì đây? Trung học hay học nghề, hay đi sản xuất? Trai gái gặp nhau bắt đầu ngập ngừng? Yêu ai đây? Yêu như thế nào? Sức khỏe tăng nhanh, kiến thức tích lũy đã khá, sống như thế nào đây? Ba câu hỏi ám ảnh: Tình yêu, nghề nghiệp, lôi sống. Không thể quy cho số phận. Cơ hội cũng chia đều sàn sàn cho mọi người.

Thanh niên ngày xưa bước vào đời như người đi xem phim đã biết trước ngồi ở rạp nào, xem phim gì, ghế số bao nhiêu, cứ thế mà ngồi vào. Ngày nay, chưa biết sẽ xem phim gì, ở rạp nào, ngồi ghế số mấy, cạnh ai. Cho đến khi ổn định được chỗ ngồi trong xã hội, xác định đúng được vai trò và vị trí của mình là phải trải qua cả một thời gian dài.

Thời gian sẽ xây dựng cho mình một niềm tin và đạo lí.

(Thanh niên và số phận – Nguyễn Khắc Viện, Ngữ Văn 11 Nâng cao, tập 2)

Đoạn trích trên sử dụng chủ yếu thao tác lập luận nào?

Câu hỏi trong đề: Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 3) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn C.

Đoạn trích so sánh cách nghĩ của thanh niên ngày xưa và ngày nay về cuộc sống.

Câu hỏi cùng đoạn

Câu 2:

Theo đoạn trích, vì sao đại đa số thanh niên thời trước không suy nghĩ, trăn trở nhiều về số phận của bản thân?

A. Họ không được tự quyết định số phận của mình

B. Họ tin vào sự sắp đặt của số mệnh

C. Họ đã biết trước số phận của mình

D. Họ luôn bằng lòng với số phận của mình

Lời giải của GV VietJack

Chọn A.

Thông tin nằm ở đoạn số 1: “Đại đa số thanh niên thời trước không ai suy nghĩ, trăn trở gì lắm về cuộc đời, vì ai đã có phận nấy.”

Câu 3:

Theo đoạn trích, vì sao thanh niên thời nay thường hay suy nghĩ, trăn trở về số phận?

A. Họ có nhiều con đường để lựa chọn

B. Sự cạnh tranh trong cuộc sống ngày càng khốc liệt

C. Họ luôn khao khát được khẳng định giá trị của bản thân

D. Những khó khăn, trắc trở trong cuộc sống dễ làm họ nản chí

Lời giải của GV VietJack

Chọn A.

Thông tin nằm ở đoạn số 3: “thanh niên ngày nay tuy cái phận mỗi người vẫn còn, song trước mặt mọi người đều có khả năng mở ra nhiều con đường.”

Câu 4:

Theo đoạn trích trên, yếu tố nào dưới đây KHÔNG có ý nghĩa quyết định đối với thành công và hạnh phúc của một con người trong thời đại ngày nay?

A. Sự lựa chọn

B. Sự cố gắng của bản thân

C. Sự hậu thuẫn của gia đình

D. Sự giúp đỡ của bạn bè

Lời giải của GV VietJack

Chọn C.

Các đáp án A, B, D đều xuất hiện trong đoạn văn số 3.

Câu 5:

Theo đoạn trích, ba yếu tố khiến thanh niên ám ảnh là gì?

A. Học hành, tình yêu, sức khỏe

B. Tình yêu, nghề nghiệp, lối sống

C. Tiền bạc, tình yêu, vị trí xã hội

D. Sức khỏe, nghề nghiệp, tình yêu

Lời giải của GV VietJack

Chọn B.

Thông tin nằm ở đoạn số 4: “Ba câu hỏi ám ảnh: Tình yêu, nghề nghiệp, lối sống”.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác ABC và M là trung điểm SC. Gọi K là giao điểm của SD với mặt phẳng (AGM). Tính $\frac{KS}{KD}$ .

A. $\frac{1}{2}$

B. $\frac{1}{3}$

C. 2

D. 3

Lời giải

Chọn A.

Gọi N là trung điểm BC, kéo dài AN cắt CD tại I. Kéo dài IM cắt SD tại K $\Rightarrow K = SD \cap (AMG)$ .

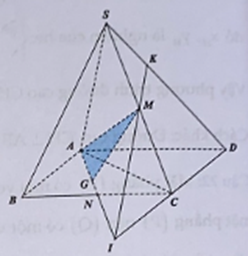
Trong không gian Oxyz, cho mặt phẳng 2x - 2y - z + 9 = 0 và mặt cầu . Tọa độ điểm M nằm trên mặt cầu (S) sao cho khoảng cách từ điểm M đến mặt phẳng (P) đạt giá trị lớn nhất là (ảnh 1)

Do N là trung điêm BC và IC // AB nên IC = AB = CD. Áp dụng định lí Menelaus cho tam giác SCD ta có

\frac{KS}{KD} . \frac{MC}{MS} . \frac{ID}{IC} = 1 \Leftrightarrow \frac{KS}{KD} . \frac{1}{1} . \frac{2}{1} = 1 \Rightarrow \frac{KS}{KD} = \frac{1}{2}

Câu 2

Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được tính theo công thức $c (t) = \frac{t}{t^{2} + 1} (mg / L)$ . Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?

Xem đáp án

Lời giải

Đáp án: 1

Với $c (t) = \frac{t}{t^{2} + 1}, t > 0$ ta có $c^{'} (t) = \frac{- t^{2} + 1}{{(t^{2} + 1)}^{2}}$ . Cho $c^{'} (t) = 0 \Leftrightarrow \frac{- t^{2} + 1}{{(t^{2} + 1)}^{2}} = 0 \Leftrightarrow t = 1$ .

Bảng biến thiên

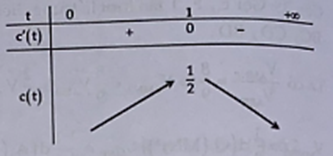
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể (ảnh 1)

Vậy $\max_{(0; + \infty)} (t) = \frac{1}{2}$ khi t = 1.

Cách khác:

Với t > 0, ta có $t^{2} + 1 \geq 2 t$ . Dấu "=" xảy ra $\Leftrightarrow t = 1$ .

Do đó,

c (t) = \frac{t}{t^{2} + 1} \leq \frac{t}{2 t} = \frac{1}{2}

. Vậy

\max_{(0; + \infty)} c (t) = \frac{1}{2}

khi t = 1.

Câu 3

Cho hình thang cong (H) giới hạn bởi các đường $y = e^{x}$ , y = 0, x = 0 và x = ln4. Đường thẳng x = k (0 < k < ln4) chia (H) thành hai phần có diện tích là $S_{1}, S_{2}$ và như hình vẽ bên. Biết với $k = \ln \frac{a}{b}$ thì $S_{1} = S_{2}$ . Tính a + b.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Câu 4

Cho cấp số cộng (U_n) có số hạng tổng quát u_n = 1 - 3n. Tổng của 10 số hạng đầu tiên của cấp số cộng bằng

A. -59048

B. -59049

C. -155

D. -310

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Câu 5

Một bệnh nhân điều trị băng đồng vị phóng xạ, dùng tia y để diệt tế bào bệnh. Thời gian chiếu xạ lần đầu là $Δ t = 20$ phút, đồng vị phóng xạ đó có chu kỳ bán rã T = 4 tháng (coi $Δ t ≪ T$ ) và vẫn dùng nguồn phóng xạ trong lần đầu. Do bệnh mới ở giai đoạn đầu nên lịch hẹn cụ thể của bệnh nhân với bác sĩ như sau:

Thời gian: 8h ngày 2/4/2021

Phương pháp điều trị: Chiếu phóng xạ

Thời gian: 8h ngày 2/5/2021

Phương pháp điều trị: Chiếu phóng xạ

Thời gian: 8h ngày 2/6/2021

Phương pháp điều trị: Chiếu phóng xạ

Hỏi lần chiếu xạ thứ 3 phải tiến hành trong bao lâu để bệnh nhân được chiếu xạ với cùng một lượng tia y như lần đầu?

A. 28,2 phút.

B. 22,2 phút.

C. 26,2 phút.

D. 24,2 phút.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Câu 6

Tìm tất cả các giá trị của tham số m để hàm số $y = x^{4} + 4 m x^{3} + 3 (m + 1) x^{2} + 1$ có cực tiểu mà không có cực đại.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Câu 7

Một chiếc ô tô chuyển động với vận tốc v(t) (m/s), có gia tốc $a (t) = v^{'} (t) = \frac{3}{t + 1} (m / s^{2})$ . Biết vận tốc của ô tô tại giây thứ 6 bằng 6 (m/s). Tính vận tốc của ô tô tại giây thứ 20 .

A. v = 3ln3

B. v = 14

C. v = 3ln3 + 6

D. v = 26

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện