Cho hình chóp S ABCD, có đáy ABCD là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ A đến (SCD).
Cho hình chóp S ABCD, có đáy ABCD là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ A đến (SCD).
Quảng cáo
Trả lời:
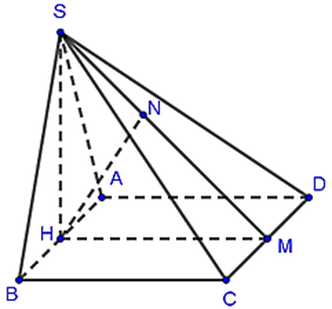
Gọi H và M lần lượt là trung điểm của AB và CD.
Tam giác SAB đều nên suy ra SH ⏊ AB.
Mà \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right.\) nên SH ⏊ (ABCD).
Kẻ HM ⏊ BD (M Î BD), kẻ HK ⏊ SM tại K.
Ta có: \[\left\{ \begin{array}{l}CD \bot HM\\CD \bot SH\;\left( {do\;SH \bot \left( {ABCD} \right)} \right)\end{array} \right.\]
\[ \Rightarrow CD \bot \left( {SHM} \right) \Rightarrow \left( {SCD} \right) \bot \left( {SHM} \right)\].
Kẻ HN ⏊ SM Þ HN ⏊ (SCD)
Do đó d(A, (SCD)) = d(H, (SCD)) = HN.
Xét tam giác SMH vuông tại H, ta có \(HM = 1;\;SH = \frac{{\sqrt 3 }}{2}\) nên
\(\frac{1}{{H{N^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{M^2}}} = \frac{1}{{{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}} + \frac{1}{{{1^2}}} = \frac{7}{3}\)
\( \Rightarrow HN = \sqrt {\frac{3}{7}} = \frac{{\sqrt {21} }}{7} \Rightarrow d\left( {A,\;\left( {SCD} \right)} \right) = d\left( {H,\;\left( {SCD} \right)} \right) = \frac{{\sqrt {21} }}{7}\).
Vậy khoảng cách từ A đến mặt phẳng (SCD) bằng \(\frac{{\sqrt {21} }}{7}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
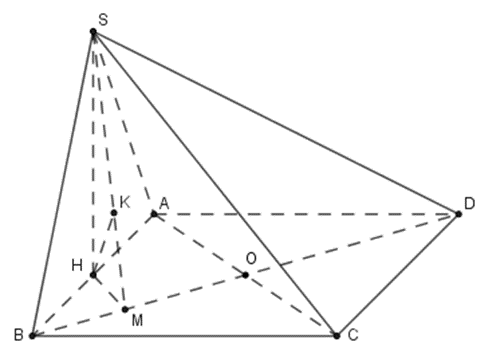
Gọi H là trung điểm của AB suy ra SH ⏊ AB .
Mà \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right.\) nên SH ⏊ (ABCD)
Gọi O = AC Ç BD.
Ta có: \(\left\{ \begin{array}{l}AC \cap \left( {SBD} \right) = O\\AO = OC\end{array} \right. \Rightarrow d\left( {C,\;\left( {SBD} \right)} \right) = d\left( {A,\;\left( {SBD} \right)} \right)\)
Lại có: \(\left\{ \begin{array}{l}AH \cap \left( {SBD} \right) = B\\AB = 2HB\end{array} \right. \Rightarrow d\left( {A,\;\left( {SBD} \right)} \right) = 2d\left( {H,\;\left( {SBD} \right)} \right)\)
\( \Rightarrow d\left( {H,\;\left( {SBD} \right)} \right) = \frac{1}{2}d\left( {A,\;\left( {SBD} \right)} \right)\)
Do đó \(\frac{{d\left( {C,\;\left( {SBD} \right)} \right)}}{{d\left( {H,\;\left( {SBD} \right)} \right)}} = \frac{{d\left( {A,\;\left( {SBD} \right)} \right)}}{{\frac{1}{2}d\left( {A,\;\left( {SBD} \right)} \right)}} = 2\).
Kẻ HM ⏊ BD (M Î BD), kẻ HK ⏊ SM tại K
Ta có: \(\left\{ \begin{array}{l}BD \bot HM\\BD \bot SH\;\left( {do\;SH \bot \left( {ABCD} \right)} \right)\end{array} \right.\)
\( \Rightarrow BD \bot \left( {SHM} \right) \Rightarrow BD \bot HK\).
Lại có HK ⏊ SM Þ HK ⏊ (SBD) tại K Þ HK = d(H, (SBD)).
Vì ABCD là hình vuông nên AO ⏊ BD mà HM ⏊ BD Þ HM // AO.
Lại có H là trung điểm của AB nên M là trung điểm của BO.
Suy ra HM là đường trung bình của tam giác ABO
\( \Rightarrow HM = \frac{{AO}}{2} = \frac{1}{2}\,.\,\frac{{a\sqrt 2 }}{2} = \frac{{a\sqrt 2 }}{4}\).
Xét tam giác SMH vuông tại H, ta có \(HM = \frac{{a\sqrt 2 }}{4};\;SH = \frac{{a\sqrt 3 }}{2}\) nên
\(\frac{1}{{H{K^2}}} = \frac{1}{{H{M^2}}} + \frac{1}{{S{H^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 2 }}{4}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{{28}}{{3{a^2}}}\)
\( \Rightarrow HK = \frac{{a\sqrt {21} }}{{14}} \Rightarrow d\left( {C,\;\left( {SBD} \right)} \right) = 2d\left( {H,\;\left( {SBD} \right)} \right) = \frac{{a\sqrt {21} }}{7}\).
Vậy khoảng cách từ C đến mặt phẳng (SBD) bằng \(\frac{{a\sqrt {21} }}{7}\).
Lời giải
Ta có: \({2^{{x^2}\, - \,x\, + \,8}} = {4^{1\, - \,3x}}\)
\( \Leftrightarrow {2^{{x^2} - x + 8}} = {2^{2\left( {1 - 3x} \right)}}\)
\( \Leftrightarrow {2^{{x^2} - x + 8}} = {2^{2 - 6x}}\)
Logarit cơ số 2 hai vế ta được: \({\log _2}{2^{{x^2} - x + 8}} = {\log _2}{2^{2 - 6x}}\)
Þ x2 − x + 8 = 2 − 6x
Û x2 + 5x + 6 = 0
\( \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = - 2\end{array} \right.\)
Vậy nghiệm của phương trình là x = −2 và x = −3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.