Trên mặt đất phẳng, người ta dựng một cây cột AB có chiều dài bằng 10 m và tạo với mặt đất góc 80°. Tại một thời điểm dưới ánh sáng mặt trời, bóng BC của cây cột trên mặt đất dài 12 m vào tạo với cây cột một góc bằng 120° (tức là ). Tính góc giữa mặt đất và đường thẳng chứa tia sáng mặt trời tại thời điểm nói trên.
Trên mặt đất phẳng, người ta dựng một cây cột AB có chiều dài bằng 10 m và tạo với mặt đất góc 80°. Tại một thời điểm dưới ánh sáng mặt trời, bóng BC của cây cột trên mặt đất dài 12 m vào tạo với cây cột một góc bằng 120° (tức là ). Tính góc giữa mặt đất và đường thẳng chứa tia sáng mặt trời tại thời điểm nói trên.
Câu hỏi trong đề: Giải SGK Toán 11 KNTT Bài tập cuối chương VII có đáp án !!
Quảng cáo
Trả lời:
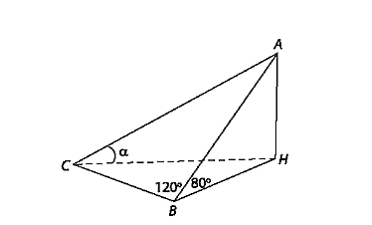
Gọi H là hình chiếu vuông góc của A lên mặt đất. Khi đó AH ^ (BCH).
Ta có góc giữa mặt đất và đường thẳng chứa tia sáng mặt trời là .
Xét tam giác AHB vuông tại H, có AH = AB × sin80° = 10 × sin80° (m).
Áp dụng định lí Côsin trong tam giác ABC, có:
AC2 = AB2 + BC2 – 2×AB×BC×cos
= 102 + 122 – 2×10×12×cos120° = 364
⇒ AC = (m).
Xét tam giác AHC vuông tại H, có .
Vậy góc giữa mặt đất và đường thẳng chứa tia sáng mặt trời tại thời điểm nói trên khoảng 31°.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
C. Số đo của góc nhị diện [S, AC, B] bằng 90°.
Lời giải
Đáp án đúng là: C
![Cho hình chóp tứ giác đều S.ABCD. Phát biểu nào sau đây là đúng? A. Số đo của góc nhị diện [S, AB, C] bằng . (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/10/blobid0-1697818239.png)
Gọi O là giao điểm của AC và BD. Kẻ OE ^ AB tại E.
Do ABCD là hình vuông nên O là trung điểm của AC và BD.
Xét tam giác ABD có OE // AD (do cùng vuông góc với AB) mà O là trung điểm của BD nên E là trung điểm của AB.
Xét tam giác SAB có SA = SB (do S.ABCD là hình chóp tứ giác đều) nên SAB là tam giác cân tại S mà SE là trung tuyến nên SE đồng thời là đường cao hay SE ^ AB.
Do đó [S, AB, C] = , suy ra A sai.
Vì ABCD là hình vuông nên BO ^ AC, S.ABCD là hình chóp đều nên SO ^ (ABCD) suy ra SO ^ AC, SO ^ BD .
Vì BO ^ AC, SO ^ AC nên [S, AC, B] = , suy ra C đúng.
Kẻ DF ^ SA tại F.
Vì SO ^ BD và AC ^ BD nên BD ^ (SAC), suy ra BD ^ SA mà DF ^ SA nên SA ^ (BDF), suy ra SA ^ BF.
Vì SA ^ BF và DF ^ SA nên [D, SA, B] = , suy ra B, D sai.
Câu 2
Lời giải
Đáp án đúng là: C
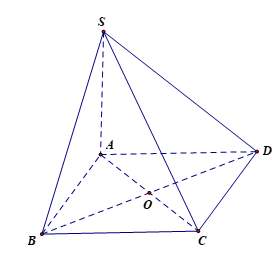
Vì ABCD là hình vuông nên AB ^ BC mà SA ^ (ABCD) nên SA ^ BC.
Có AB ^ BC và SA ^ BC nên BC ^ (SAB). Vậy A đúng.
Vì ABCD là hình vuông nên AC ^ BD mà SA ^ (ABCD) nên SA ^ BD.
Có AC ^ BD và SA ^ BD nên BD ^ (SAC). Vậy B đúng.
Vì ABCD là hình vuông nên AD ^ AB mà SA ^ (ABCD) nên SA ^ AD.
Có AD ^ AB và SA ^ AD nên AD ^ (SAB). Vậy D đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.