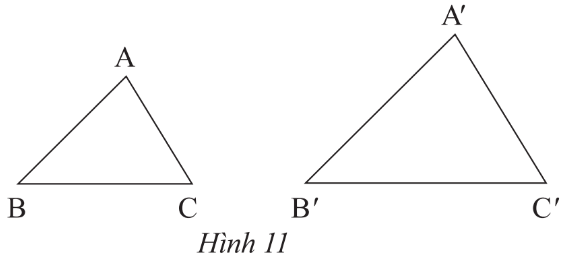
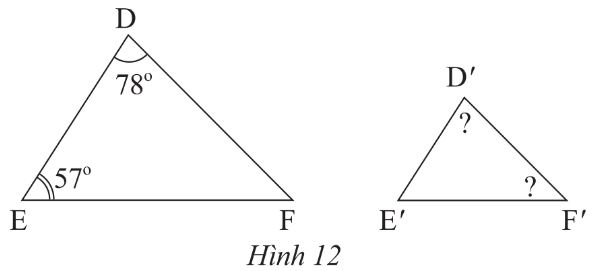
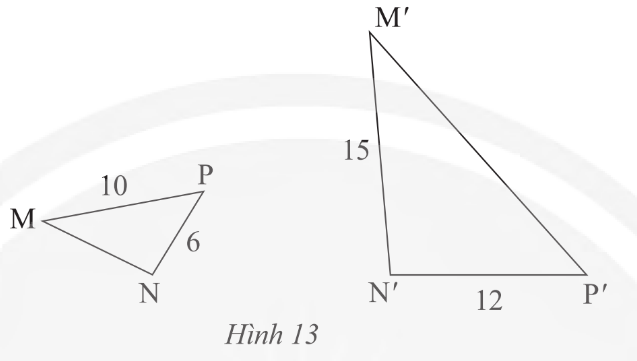
Cho tam giác ABC và tam giác A'B'C' như Hình 2.
a) Hãy viết các cặp góc bằng nhau.
b) Tính và so sánh các tỉ số \[\frac{{A'B'}}{{AB}};\;\;\frac{{A'C'}}{{AC}};\;\frac{{B'C'}}{{BC}}\].

Cho tam giác ABC và tam giác A'B'C' như Hình 2.
a) Hãy viết các cặp góc bằng nhau.
b) Tính và so sánh các tỉ số \[\frac{{A'B'}}{{AB}};\;\;\frac{{A'C'}}{{AC}};\;\frac{{B'C'}}{{BC}}\].

Câu hỏi trong đề: Giải SGK Toán 8 Bài 1. Hai tam giác đồng dạng có đáp án !!
Quảng cáo
Trả lời:
Lời giải:
a) Từ các kí hiệu trên hình vẽ, ta thấy các cặp góc bằng nhau: \[\widehat A = \widehat {A'};\;\widehat B = \widehat {B';}\;\widehat C = \widehat {C'}\].
b) • \[\frac{{A'B'}}{{AB}} = \frac{6}{4} = \frac{3}{2}\];
• \[\frac{{A'C'}}{{AC}} = \frac{{7,5}}{5} = \frac{3}{2}\];
• \[\frac{{B'C'}}{{BC}} = \frac{9}{6} = \frac{3}{2}\].
Vậy \[\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
a) Do ΔABC ᔕ ΔDEF nên \[\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}} = \frac{{AC}}{{DF}} = \frac{2}{5}\]
• Chu vi tam giác ABC là:
\[{P_{ABC}} = AB + BC + AC = \frac{2}{5}\left( {DE + EF + DF} \right)\]
• Chu vi tam giác DEF là:
\[{P_{DEF}} = DE + EF + DF\]
Tỉ số chu vi của hai tam giác ABC và DEF là:
\[\frac{{{P_{ABC}}}}{{{P_{DEF}}}} = \frac{{\frac{2}{5}\left( {DE + EF + DF} \right)}}{{DE + EF + DF}} = \frac{2}{5}\].
Vậy tỉ số chu vi của hai tam giác đã cho là \[\frac{2}{5}\].
b) Ta có: \[\frac{{{P_{ABC}}}}{{{P_{DEF}}}} = \frac{2}{5}\]
Mà \[{P_{DEF}} - {P_{ABC}} = 36\]
Do đó \[{P_{ABC}} = 24\;cm;\,\,{P_{DEF}} = 60\;cm\].
Vậy chu vi tam giác ABC là 24 cm và chu vi tam giác DEF là 60 cm.Lời giải
Lời giải:
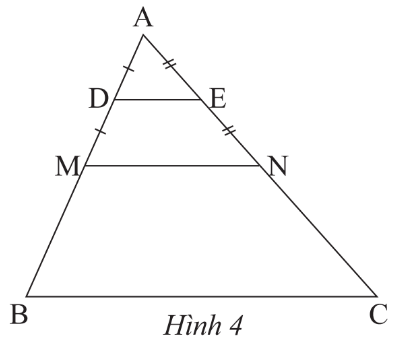
Ta có: ΔADE ᔕ ΔAMN, ΔAMN ᔕ ΔABC suy ra ΔADE ᔕ ΔABC.
• Vì ΔADE ᔕ ΔAMN theo tỉ số \[\frac{{AD}}{{AM}} = \frac{1}{2}\] (vì DE là đường trung bình tam giác AMN).
• Vì ΔAMN ᔕ ΔABC theo tỉ số \[\frac{{AM}}{{AB}} = \frac{1}{2}\] (vì MN là đường trung bình tam giác ABC).
• Vì ΔADE ᔕ ΔABC theo tỉ số \[\frac{{AD}}{{AB}} = \frac{{\frac{1}{2}AM}}{{2AM}} = \frac{1}{4}\] (vì MN là đường trung bình tam giác ABC).
Vậy tam giác ADE đồng dạng tam giác ABC theo tỉ số đồng dạng là \[\frac{1}{4}\].
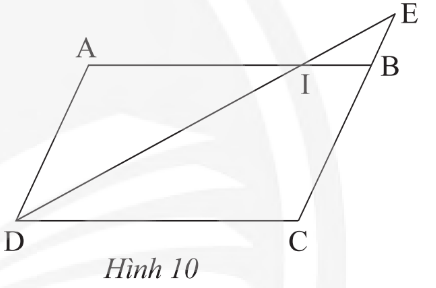
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
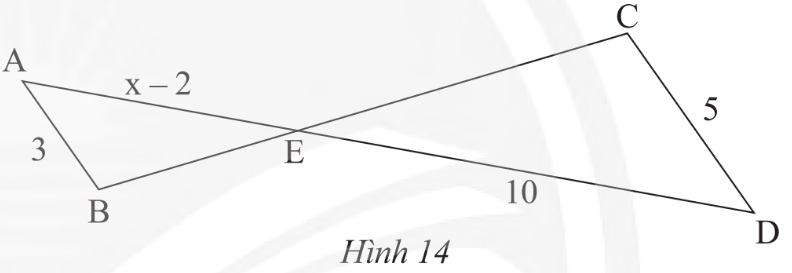
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
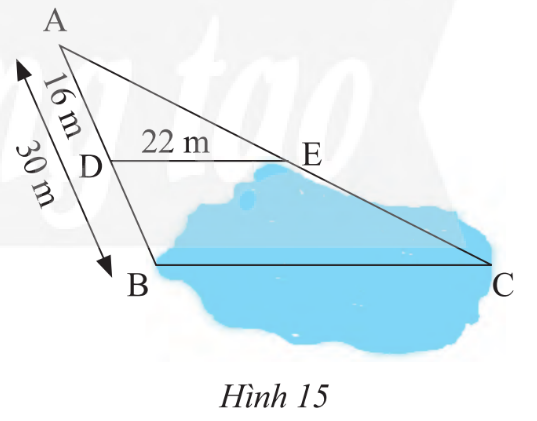
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.