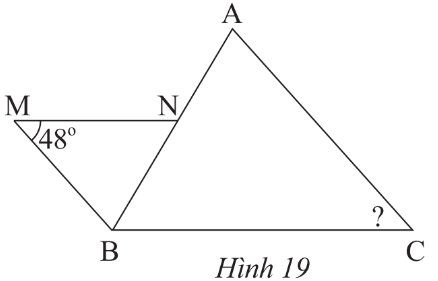
Cho tam giác ABC và tam giác A'B'C' có các kích thước như Hình 1. Trên cạnh AB và AC của tam giác ABC lần lượt lấy hai điểm M, N sao cho AM = 2 cm, AN = 3 cm.
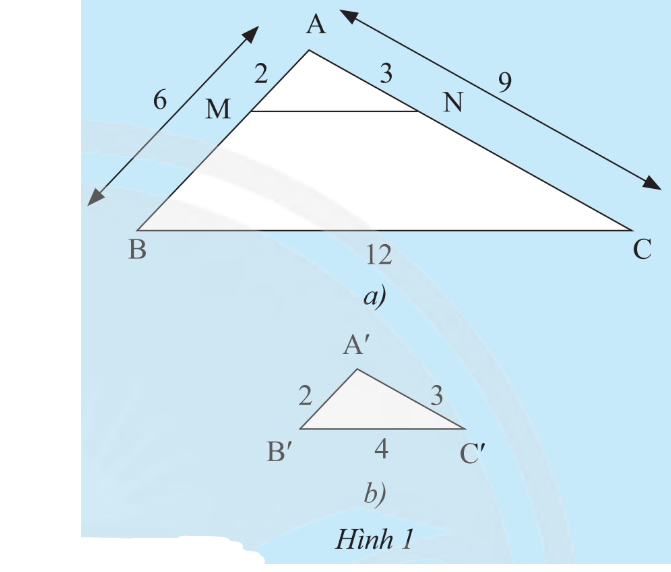
a) So sánh các tỉ số \[\frac{{A'B'}}{{AB}},\;\frac{{A'C'}}{{AC}},\;\frac{{B'C'}}{{BC}}\].
b) Tính độ dài đoạn thẳng MN.
c) Em có nhận xét gì về mối quan hệ giữa các tam giác ABC, AMN và A'B'C'.
Cho tam giác ABC và tam giác A'B'C' có các kích thước như Hình 1. Trên cạnh AB và AC của tam giác ABC lần lượt lấy hai điểm M, N sao cho AM = 2 cm, AN = 3 cm.

a) So sánh các tỉ số \[\frac{{A'B'}}{{AB}},\;\frac{{A'C'}}{{AC}},\;\frac{{B'C'}}{{BC}}\].
b) Tính độ dài đoạn thẳng MN.
c) Em có nhận xét gì về mối quan hệ giữa các tam giác ABC, AMN và A'B'C'.
Quảng cáo
Trả lời:
Lời giải:
a) Ta có: \[\frac{{A'B'}}{{AB}} = \frac{2}{6} = \frac{1}{3}\];
\[\frac{{A'C'}}{{AC}} = \frac{3}{9} = \frac{1}{3}\];
\[\frac{{B'C'}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\].
Do đó \[\frac{{A'B'}}{{AB}} = \;\frac{{A'C'}}{{AC}} = \;\frac{{B'C'}}{{BC}} = \frac{1}{3}\].
b) Tam giác ABC có \[\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{3}\], theo định lí Thalès đảo suy ra MN // BC.
Khi đó ΔAMN ᔕ ΔABC nên \[\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{3}\] suy ra MN = 4.
c) Xét tam giác AMN và A'B'C' có:
• MN = B'C' = 4;
• AM = A'B' = 2;
• AN = A'C' = 3.
Suy ra ΔAMN = ΔA′B′C′ (c.c.c).
Nhận xét: ΔAMN = ΔA′B′C′, ΔA′B′C′ ᔕ ΔABC và ΔAMN ᔕ ΔABC.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
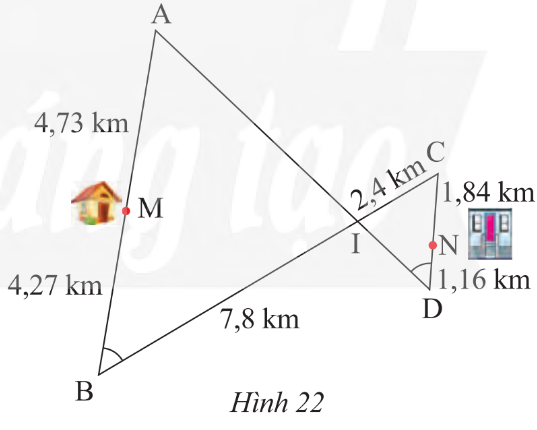
Xét ΔIAB và ΔICD ta có:
\[\widehat B = \widehat {D\;}\] (gt)
\[\widehat {AIB} = \widehat {CID}\] (đối đỉnh)
Suy ra ΔIAB ᔕ ΔICD (g.g) nên \[\frac{{IA}}{{TC}} = \frac{{IB}}{{ID}} = \frac{{AB}}{{CD}}\]
\[ \Rightarrow \frac{{IA}}{{2,4}} = \frac{{7,8}}{{ID}} = \frac{9}{3} = 3\;\] ⇒ IA = 7,2; ID = 2,6
Quãng đường đi từ M → A → I là: 4,73 + 7,2 = 11,93 (km)
Quãng đường đi từ M → B → I là: 4,27 + 7,8 = 12,07 (km)
Quãng đường đi từ I → C → N là: 2,4 + 1,84 = 4,24 (km)
Quãng đường đi từ I → D → N là: 2,6 + 1,16 = 3,76 (km)
Vậy quãng đường ngắn nhất để đi từ nhà của anh Thanh đến công ty là M → A → I → D → N với độ dài 15,69 km.
Lời giải
Lời giải:
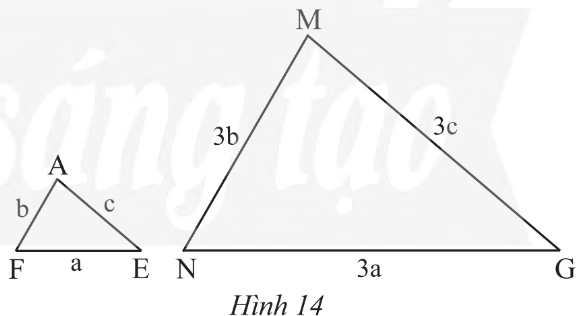
Chu vi tam giác ABC: AB + AC + BC = 19.
Tỉ số chu vi của hai tam giác ABC và A'B'C' là: \[k = \frac{{19}}{{66,5}} = \frac{2}{7}\].
ΔABC ᔕ ΔA′B′C′ nên \[\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{2}{7}\].
Vậy: A′B′=14, A′C′=21, \[B'C' = \frac{{63}}{2}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.