Câu hỏi:
13/07/2024 4,346
a) Trong Hình 20a, cho biết \[\widehat N = \widehat E,\;\widehat M = \widehat D\], MP = 18 m, DF = 24 m, EF = 32 m, NP = a + 3 (m). Tìm a.
b) Cho ABCD là hình thang (AB // CD) (Hình 20b).
Chứng minh rằng ΔAMB ᔕ ΔCMD. Tìm x, y.
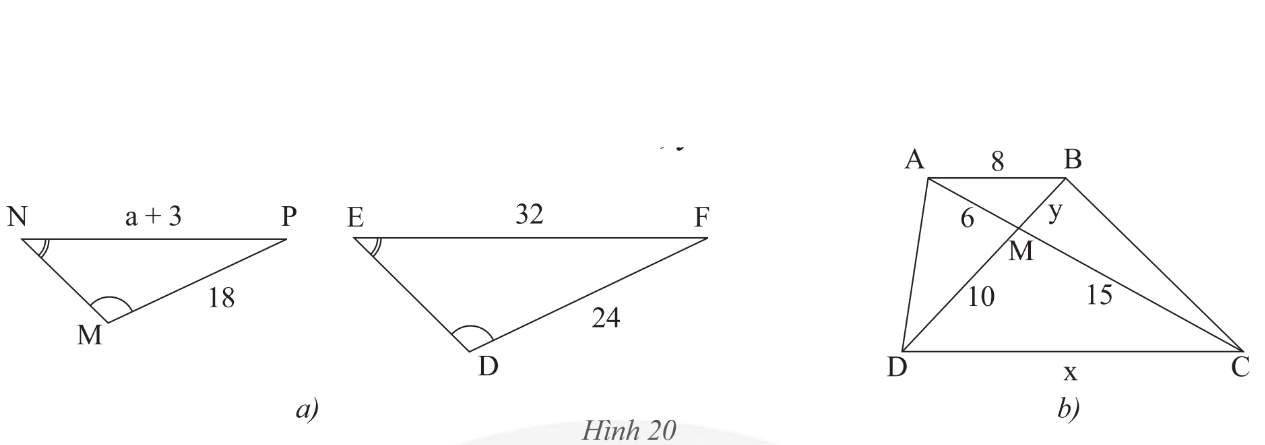
a) Trong Hình 20a, cho biết \[\widehat N = \widehat E,\;\widehat M = \widehat D\], MP = 18 m, DF = 24 m, EF = 32 m, NP = a + 3 (m). Tìm a.
b) Cho ABCD là hình thang (AB // CD) (Hình 20b).
Chứng minh rằng ΔAMB ᔕ ΔCMD. Tìm x, y.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
a) Xét ΔMNP và ΔDEF có:
\[\widehat N = \widehat E,\;\widehat M = \widehat D\]
Do đó ΔMNP ᔕ ΔDEF (g.g)
Suy ra \[\frac{{NP}}{{EF}} = \frac{{MP}}{{DF}}\] (các cạnh tương ứng).
Khi đó \[\frac{{a + 3}}{{32}} = \frac{{18}}{{24}} = \frac{3}{4}\] nên \[a + 3 = \frac{{32\,.\,\,3}}{4} = 24\] (cm).
Vậy a = 24 – 3 = 21.
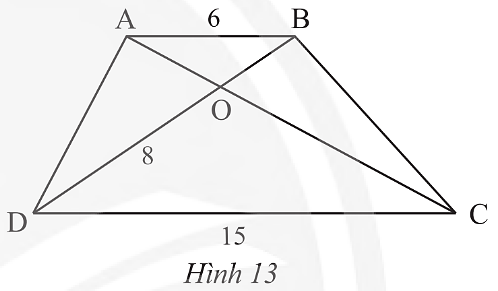
b) Xét hình thang ABCD (AB // CD):
Vì AB // CD nên \[\widehat {MAB} = \widehat {MCD},\;\widehat {MBA} = \widehat {MDC}\;\] (cặp góc so le trong).
Xét ΔAMB và ΔCMD có:
\[\widehat {MAB} = \widehat {MCD}\;\] (chứng minh trên)
\[\widehat {MBA} = \widehat {MDC}\] (chứng minh trên)
Do đó ΔAMB ᔕ ΔCMD (g.g)
Suy ra \[\frac{{AM}}{{CM}} = \frac{{MB}}{{MD}} = \frac{{AB}}{{CD}}\] (các cặp cạnh tương ứng).
Khi đó \[\frac{6}{{15}} = \frac{y}{{10}} = \frac{8}{x}\].
Suy ra \[x = \frac{{15\,.\,8}}{6} = 20;y = \frac{{6\,.\,10}}{{15}} = 4\].
Vậy x = 20; y = 4.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
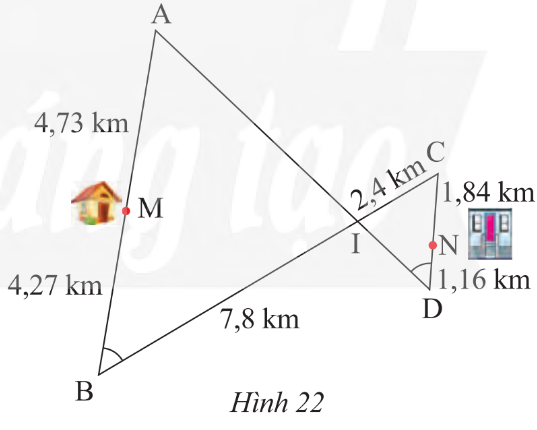
Xét ΔIAB và ΔICD ta có:
\[\widehat B = \widehat {D\;}\] (gt)
\[\widehat {AIB} = \widehat {CID}\] (đối đỉnh)
Suy ra ΔIAB ᔕ ΔICD (g.g) nên \[\frac{{IA}}{{TC}} = \frac{{IB}}{{ID}} = \frac{{AB}}{{CD}}\]
\[ \Rightarrow \frac{{IA}}{{2,4}} = \frac{{7,8}}{{ID}} = \frac{9}{3} = 3\;\] ⇒ IA = 7,2; ID = 2,6
Quãng đường đi từ M → A → I là: 4,73 + 7,2 = 11,93 (km)
Quãng đường đi từ M → B → I là: 4,27 + 7,8 = 12,07 (km)
Quãng đường đi từ I → C → N là: 2,4 + 1,84 = 4,24 (km)
Quãng đường đi từ I → D → N là: 2,6 + 1,16 = 3,76 (km)
Vậy quãng đường ngắn nhất để đi từ nhà của anh Thanh đến công ty là M → A → I → D → N với độ dài 15,69 km.
Lời giải
Lời giải:
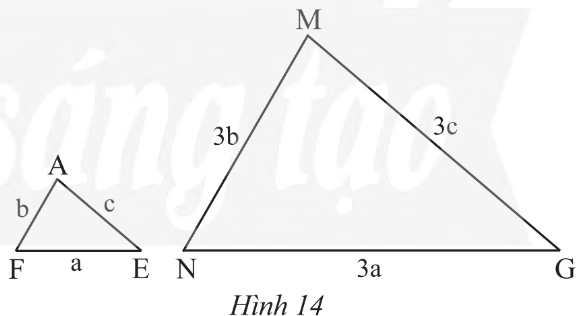
Chu vi tam giác ABC: AB + AC + BC = 19.
Tỉ số chu vi của hai tam giác ABC và A'B'C' là: \[k = \frac{{19}}{{66,5}} = \frac{2}{7}\].
ΔABC ᔕ ΔA′B′C′ nên \[\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{2}{7}\].
Vậy: A′B′=14, A′C′=21, \[B'C' = \frac{{63}}{2}\].
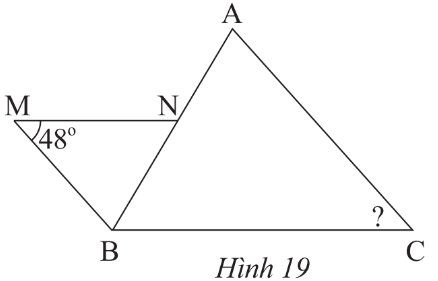
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
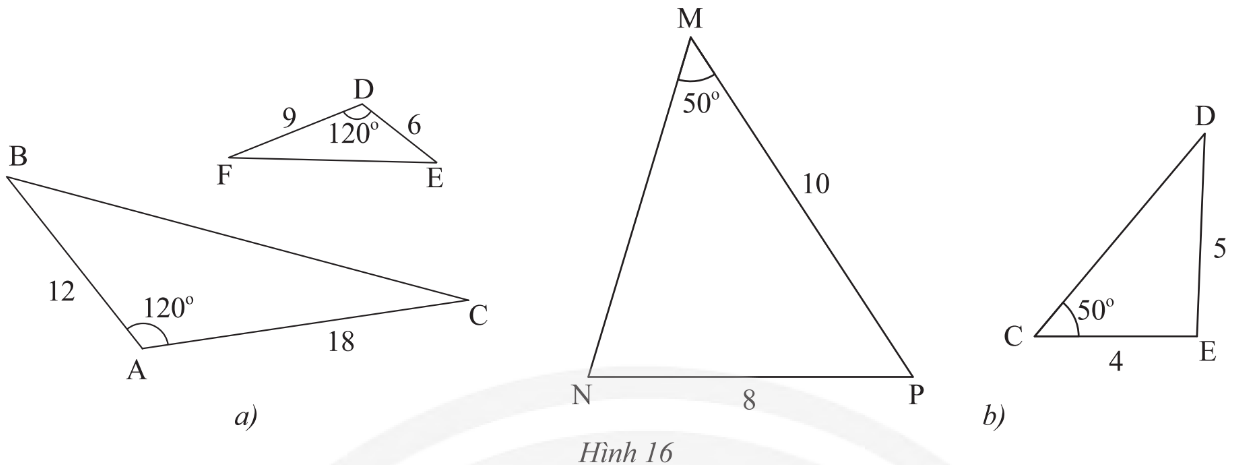
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 2
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận