Quảng cáo
Trả lời:
Lời giải:
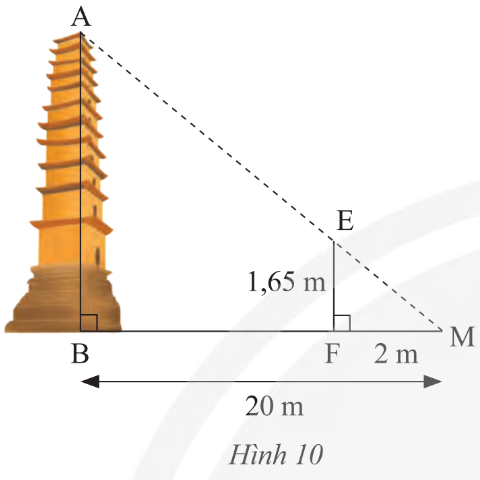
Xét ta giác vuông MEF và MAB ta có: \[\widehat M\] chung
Suy ra ΔMEF ᔕ ΔMAB (g.g) nên \[\frac{{EF}}{{AB}} = \frac{{MF}}{{MB}}\] (các cạnh tương ứng).
Khi đó \[\frac{{1,65}}{{AB}} = \frac{2}{{20}}\;\]suy ra \[AB = \frac{{1,65\,.\,20}}{2} = 16,5\;\] (cm).
Vậy AB = 16,5 (cm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
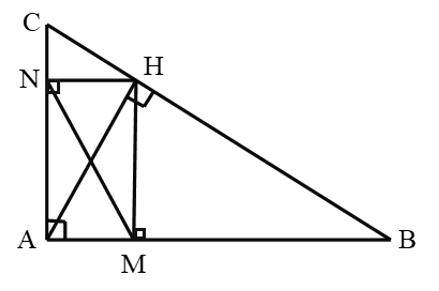
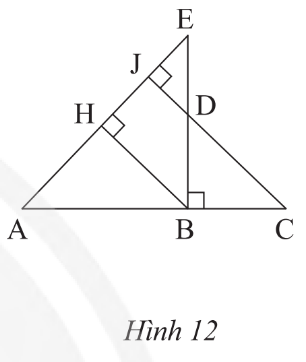
a) Xét hai tam giác vuông AMH và AHB có: \[\widehat A\] chung
Suy ra ΔAMH ᔕ ΔAHB (g.g)
b) ΔAMH ᔕ ΔAHB nên \[\frac{{AM}}{{AH}} = \frac{{AH}}{{AB}}\;\] hay AM.AB = AH2 (1)
Xét hai tam giác vuông ANH và AHC có: \[\widehat A\] chung
Suy ra ΔANH ᔕ ΔAHC (g.g) nên \[\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}\;\] hay AN.AC = AH2 (2)
Từ (1) và (2) suy ra AM.AB = AN.AC (đpcm).
c) Ta có AM.AB = AN.AC, do đó \[\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\].
Xét hai tam giác vuông AMN và ABC có:
\[\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\] (chứng minh trên)
Do đó ΔANM ᔕ ΔABC (c.g.c)
d) Áp dụng định lí Pythagore vào tam giác ABC, ta có:
BC2 = AB2 + AC2 = 92 + 122 = 225.
Suy ra BC = 15 cm.
Xét hai tam giác vuông ABC và HBA có \(\widehat B\) chung
Do đó ΔABC ᔕ ΔHBA (g.g).
Suy ra \[\frac{{AC}}{{AH}} = \frac{{BC}}{{AB}}\] (các cặp cạnh tương ứng).
Khi đó AH.BC = AB.AC hay AH.15 = 9.12.
Suy ra AH = 7,2 cm.
• Từ (1): AM.AB = AH2 nên \[AM = \frac{{A{H^2}}}{{AB}} = \frac{{7,{2^2}}}{9} = 5,76\,\,(cm)\]
• Từ (2): AN.AC = AH2 nên \[AN = \frac{{A{H^2}}}{{AC}} = \frac{{7,{2^2}}}{{12}} = 4,32\,\,(cm)\]
Diện tích tam giác AMN là:
\[\frac{1}{2}\,.\,5,76\,.\,4,32 = 12,4416\,\,(c{m^2})\].
Vậy diện tích tam giác AMN là 12,4416 cm2.
Lời giải
Lời giải:
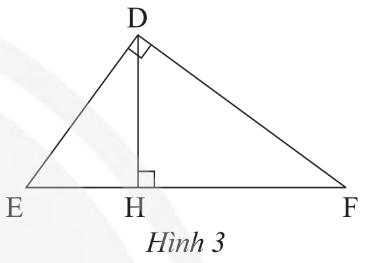
Tam giác HED vuông tại H và tam giác DEF vuông tại D có chung
Do đó ΔHED ᔕ ΔDEF (g.g)
Suy ra (các cạnh tương ứng).
Do đó DE2 = EH.EF (đpcm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Tấn Dũng ッ
16,5 m mà sao lại 16,5 cm