Câu hỏi:
04/12/2023 1,290
Cho tam giác ABC vuông tại A, kẻ đường phân giác BM. Trên cạnh BC lấy điểm D sao cho BD = BA. Gọi H là hình chiếu vuông góc của D trên AC, K là hình chiếu vuông góc của A trên DM. Cho các phát biểu sau:
(I) BM là đường trung trực của AD;
(II) AK, DH, BM đồng quy tại một điểm;
(III) AK // BC.
Khẳng định nào sau đây là đúng?
Cho tam giác ABC vuông tại A, kẻ đường phân giác BM. Trên cạnh BC lấy điểm D sao cho BD = BA. Gọi H là hình chiếu vuông góc của D trên AC, K là hình chiếu vuông góc của A trên DM. Cho các phát biểu sau:
(I) BM là đường trung trực của AD;
(II) AK, DH, BM đồng quy tại một điểm;
(III) AK // BC.
Khẳng định nào sau đây là đúng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D
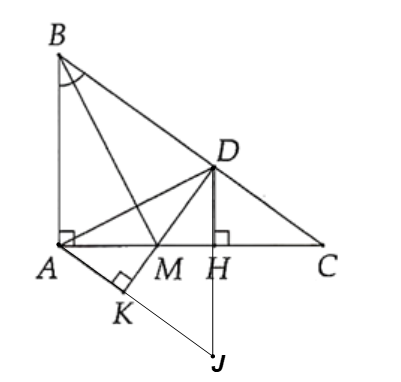
Vì BD = BA do đó tam giác ABD cân tại B.
Nên BM là đường phân giác cũng là đường trung trực của cạnh AD trong tam giác.
Suy ra BM ⊥ AD (1)
Kéo dài AK cắt DH tại J.
Khi đó ∆ADJ có AH ⊥ DJ, DK ⊥ AJ và AH cắt DK tại M nên M là trực tâm của ∆ADJ.
Suy ra JM ⊥ AD (2)
Từ (1) và (2) suy ra ba điểm B, M, J thẳng hàng hay AK, BM, DH là ba đường đồng quy.
Do BM là đường trung trực của AD nên MA = MD.
Xét ∆BAM và ∆BDM có:
BM là cạnh chung; BA = BD (giả thiết); MA = MD (chứng minh trên)
Do đó ∆BAM = ∆BDM (c.c.c)
Suy ra (hai góc tương ứng)
Mà nên hay MD ⊥ BC, tức DK ⊥ BC.
Lại có DK ⊥ AK tại K nên AK // BC.
Vậy cả (I), (II) và (III) đều đúng. Ta chọn phương án D.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
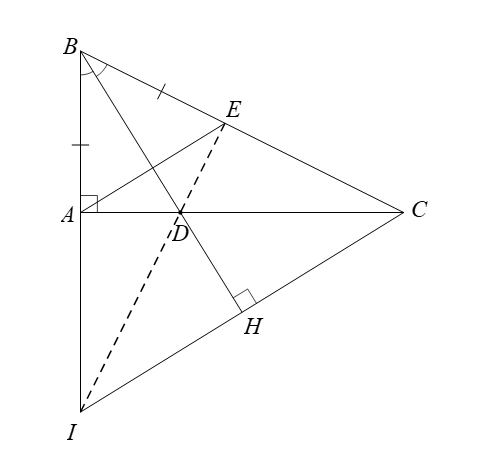
Gọi I là giao điểm của CH và AB.
Xét ∆IBC có CA ⊥ BI, BH ⊥ CI và CA cắt BH tại D nên D là trực tâm của ∆IBC.
Suy ra ID ⊥ BC (1)
Xét ∆BAD và ∆BED có:
BA = BE (giả thiết);
(do BD là đường phân giác)
BD là cạnh chung
Do đó ∆BAD = ∆BED (c.g.c).
Suy ra (hai góc tương ứng) (do
Hay DE ⊥ BC (2)
Từ (1) và (2) suy ra I, D, E thẳng hàng hay BA, DE, CH đồng quy.
Vậy đường thẳng DE đi qua giao điểm của AB và CH và ba đường thẳng BA, DE, CH đồng quy.
Do đó không có khẳng định nào sai. Ta chọn phương án A.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D
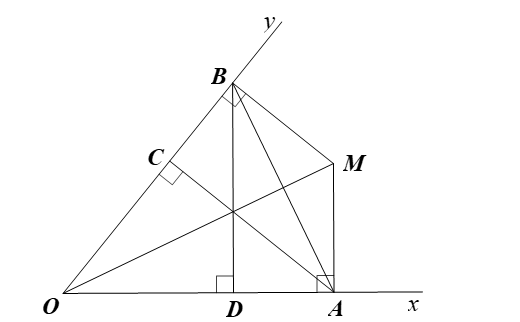
Xét ∆AOM và ∆BOM có:
OM là cạnh chung;
OA = OB (giả thiết)
Do đó ∆AOM = ∆BOM (cạnh huyền – cạnh góc vuông).
Suy ra MA = MB (hai cạnh tương ứng).
Nên M nằm trên đường trung trực của AB.
Lại có OA = OB nên O nằm trên đường trung trực của AB.
Do đó OM là đường trung trực của AB, nên OM ⊥ AB.
Xét ∆AOB có ba đường cao OM, AC, BD nên ba đường này đồng quy tại một điểm.
Vậy cả A và B đều là khẳng định đúng.
Khi đó phương án D là sai. Ta chọn phương án D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 02
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận