Câu hỏi:

19/08/2025 4,820

Cho đường thẳng (d): y = ax + b. Tìm a và b để đường thẳng (d) song song với đường thẳng (d'): y = 5x + 3 và đi qua điểm A(1;3)

Xem lời giải

Câu hỏi trong đề: Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 5) !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có (d) song song với (d') ta có a = 5 và

Lại có (d) di qua A(1;3) nên $3 = 1 \cdot a + b \Rightarrow 3 - 1 \cdot 5 + b \Leftrightarrow b = - 2$ .

Vậy a = 5 và b = -2

Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC có ba góc nhọn và các đường cao AF, BD, CE cắt nhau tại H

1) Chứng minh rằng $\hat{D A H} = \hat{D E H} .$

2) Gọi O và M lần lượt là trung điểm của BC và AH. Chứng minh rằng tứ giác MDOE nội tiếp.

3) Gọi K là giao điểm của AH và DE. Chứng minh rằng: AH² = 2MK.(AF + HF)

Xem đáp án

Lời giải

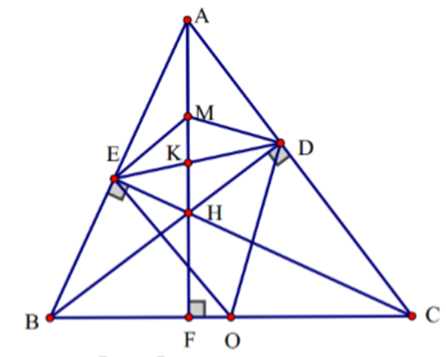
Cho tam giác ABC có ba góc nhọn và các đường cao AF, BD, CE cắt nhau tại H 1) Chứng minh rằng góc dah = góc deh (ảnh 1)

a) Vì BD, CE là đường cao nên $\hat{B D A} = \hat{C E A} = 90 ° .$

Tứ giác ADHE có

$\hat{H D A} + \hat{H E A} = 90 ° + 90 ° = 180 °$

Nên ADHE nội tiếp đường tròn, suy ra $\hat{D A H} = \hat{D E H}$ (hai góc nội tiếp cùng chắn cung HE

Vậy

\hat{D A H} = \hat{D E H} .

2) Tam giác ADE vuông tại D có DM là trung tuyến (là trung điểm AH), suy ra $M D = M A = M H = \frac{A H}{2} .$

Tương tự $M E = M A = M H = \frac{A H}{2} .$

Suy ra MD = MA = MH = ME nên tam giác MAD cân tại M suy ra $\hat{M D A} = \hat{M A D} .$

Tương tự $\hat{O D C} = \hat{O C D} .$ Do đó: $\hat{M D A} + \hat{O D C} = \hat{M A D} + \hat{O C D} = 90 ° .$ Suy ra $\hat{M D O} = 90 ° .$

Tương tự, ta chứng minh được $\hat{M E O} = 90 ° .$

Tứ giác MDOE có $\hat{M D O} + \hat{M E O} = 90 ° + 90 ° = 180 °$ nên tứ giác MDOE nội tiếp đường tròn.

3) Ta có $A H^{2} = 2 M π \cdot (A F + H F)$

$\Leftrightarrow A H^{2} - 2 M K \cdot (A H + H F + H F) (1) \Leftrightarrow 4 M H^{2} - 2 M K \cdot (2 H M + 2 H F) \Leftrightarrow M H^{2} - M K \cdot H M + M K \cdot H F \Leftrightarrow M H^{2} - M K \cdot H M - M K \cdot H F \Leftrightarrow M H \cdot (M H - M K) = M K \cdot H F \Leftrightarrow M H \cdot H K = M K \cdot H F$

$Δ D K M ∽ Δ F D M$ suy ra $\frac{M K}{M D} = \frac{D K}{D H} (2)$

Vì (2) được chứng minh nên (1) được chứng minh.

Câu 2

Một đội công nhân phải trồng 96 cây xanh. Đội dự định chia đều số cây cho mỗi công nhân nhưng khi chuẩn bị trồng thì có 4 công nhân được điều đi làm việc khác nên mỗi công nhân còn lại phải trồng thêm 4 cây. Hỏi lúc đầu đợi công nhân có bao nhiêu người?

Xem đáp án

Lời giải

Gọi x (người) là số công nhân lúc đầu của đội $(x > 4, x \in ℕ) .$

Số công nhân làm việc thực tế là x - 4 (người).

Số cây xanh mỗi công nhân trồng theo dự định là $\frac{96}{x}$ (cây).

Số cây xanh mỗi công nhân trồng theo thực tế là $\frac{96}{x - 4}$ (cây).

Do mỗi công nhân còn lại phải trồng thêm 4 cây nên ta có phương trình:

$\frac{96}{x - 4} - \frac{96}{x} = 4 \Leftrightarrow \frac{1}{x - 4} - \frac{1}{x} = \frac{1}{24} \Leftrightarrow \frac{x - (x - 4)}{x (x - 4)} = \frac{1}{24} \Leftrightarrow \frac{4}{x^{2} - 4 x} = \frac{1}{24} \Rightarrow x^{2} - 4 x - 96 = 0 \Leftrightarrow (x + 8) (x - 12) = 0 \Leftrightarrow [\begin{array}{l} x = - 8 \\ x = 12 \end{array} .$

Đối chiều điều kiện và thử lại ta thấy x = 12 thỏa mãn.

Vậy số công nhân lúc đầu của đội là 12 người.

Câu 3

Rút gọn biểu thức: $A = \sqrt{x} \cdot (\frac{1}{x - \sqrt{x}} + \frac{1}{\sqrt{x} - 1}) : \frac{\sqrt{x} + 1}{x - 2 \sqrt{x} + 1}$ với $x > 0, x \neq 1.$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho a, b, c là các số thực dương. Chứng minh rằng:

$a^{2} + b^{2} + 2 a b c + c^{2} + 1 \geq 2 (a b + a c + b c) .$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho parabol $(P) : y = x^{2}$ và đường thẳng $(d) : y = 3 x + m .$ Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ $x_{1}, x_{2}$ thỏa mãn $x_{1} + 2 x_{2} = m + 3.$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Giải hệ phương trình: $\{\begin{cases} 3 x + y = 5 \\ 2 x + 5 y = 12 \end{cases} .$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Rút gọn biểu thức: $A = \sqrt{x} \cdot (\frac{1}{x - \sqrt{x}} + \frac{1}{\sqrt{x} - 1}) : \frac{\sqrt{x} + 1}{x - 2 \sqrt{x} + 1}$ với $x > 0, x \neq 1.$

Cho a, b, c là các số thực dương. Chứng minh rằng:

$a^{2} + b^{2} + 2 a b c + c^{2} + 1 \geq 2 (a b + a c + b c) .$

Cho parabol $(P) : y = x^{2}$ và đường thẳng $(d) : y = 3 x + m .$ Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ $x_{1}, x_{2}$ thỏa mãn $x_{1} + 2 x_{2} = m + 3.$

Giải hệ phương trình: $\{\begin{cases} 3 x + y = 5 \\ 2 x + 5 y = 12 \end{cases} .$