Câu hỏi:

13/07/2024 5,386

Cho tam giác ABC vuông tại A, trên cạnh AB lấy điểm M (M khác A, M khác B). Từ điểm M vẽ đường thẳng MN vuông góc với BC (N thuộc BC), đường thẳng MN cắt đường thẳng AC tại K.

1) Chứng minh tứ giác AMNC nội tiếp.

2) Chứng minh $\hat{A B K} = \hat{A C M} .$

3) Đoạn thẳng BKcắt đường tròn đường kính BM tại điểm D (D khác B). Gọi I là tâm và r là bán kính của đường tròn nội tiếp tam giác BKC. Chứng minh $\frac{1}{r} = \frac{1}{K N} + \frac{1}{C D} + \frac{1}{A B} \cdot$

Xem lời giải

Câu hỏi trong đề: Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 8) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Cho tam giác ABC vuông tại A, trên cạnh AB lấy điểm M (M khác A, M khác B). Từ điểm M vẽ đường thẳng MN vuông góc với BC (N thuộc BC), đường thẳng MN cắt đường thẳng AC tại K. (ảnh 1)

1) Xét tứ giác AMNC có

$\hat{C A M} = \hat{C A B} = 90 °$ ( $Δ A B C$ vuông tại $A, M \in A B$ ).

$\hat{C N M} = 90 °$ ( $M N ⊥ B C$ ).

Suy ra $\hat{C A M} + \hat{C N M} = 90 ° + 90 ° = 180 °$ .

Vậy tứ giác AMNC nội tiếp (tổng hai góc đối bằng 180^o ).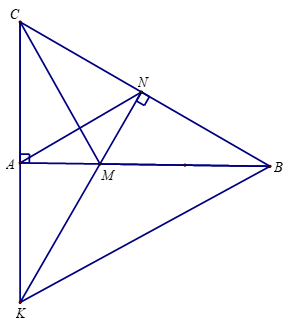

Xét ANBK có

$\hat{K A B} = 90 °$ (kề bù với góc vuông CAB).

$\hat{K N B} = \hat{M N B} = 90 °$ (MN vuông góc BC, K thuộc đường thẳng MN).

Suy ra $\hat{K A B} = \hat{K N B} = 90 ° .$

Do đó tứ giác ANBK nội tiếp (hai đỉnh A, N kề nhau cùng nhìn cạnh BK dưới một góc bằng 90^o )

Suy ra $\hat{A B K} = \hat{A N K}$ (hai góc nội tiếp cùng chắn cung AK) (1)

Vì tứ giác AMNC nội tiếp (chứng minh câu 5.1)

nên $\hat{A N M} = \hat{A C M}$ (hai góc nội tiếp cùng chắn cung AM).

hay $\hat{A N K} = \hat{A C M}$ (K thuộc đường thẳng MN) (2)

Từ (1) và (2) suy ra $\hat{A B K} = \hat{A C M} .$

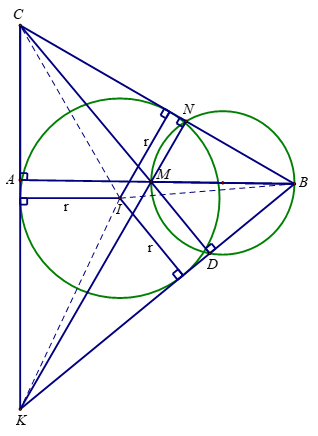
Xét $Δ B C K$ có BA là đường cao, KN là đường cao, M là giao điểm của BA và K

Suy ra M là trực tâm của $Δ B C K .$

Do đó $C M ⊥ B K$ (1)

Xét đường tròn đường kính BM có $\hat{M D B} = 90 °$ (góc nội tiếp chắn nửa đường tròn).

Suy ra $M D ⊥ B K$ (2)

Từ (1) và (2) suy ra ba điểm C, M, D thẳng hàng. Do đó

C D ⊥ B K .

Diện tích $Δ B I C$ là $S_{B I C} = \frac{1}{2} . r . B C$ .

Diện tích $Δ B I K$ là $S_{B I K} = \frac{1}{2} . r . B K$ .

Diện tích $Δ C I K$ là $S_{C I K} = \frac{1}{2} . r . C K$ .

Diện tích $Δ B C K$ là $S_{B C K} = \frac{1}{2} K N . B C = \frac{1}{2} B K . C D = \frac{1}{2} C K . A B$ .

Suy ra $\frac{1}{2} B C = \frac{S_{B C K}}{K N}; \frac{1}{2} B K = \frac{S_{B C K}}{C D}; \frac{1}{2} C K = \frac{S_{B C K}}{A B}$ .

Mà $S_{B C K} = S_{B I C} + S_{B I K} + S_{C I K}$

Hay $S_{B C K} = r \cdot \frac{S_{B C K}}{K N} + r \cdot \frac{S_{B C K}}{C D} + r \cdot \frac{S_{B C K}}{A B}$

Do đó $S_{B C K} = r . S_{B C K} (\frac{1}{K N} + \frac{1}{C D} + \frac{1}{A B})$

Vậy $\frac{1}{r} = \frac{1}{K N} + \frac{1}{C D} + \frac{1}{A B} \cdot$

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Cấp tốc 789+ thi vào lớp 10 môn Toán

Đã bán 261

₫ 195.000 ₫ 95.000

Hà Nội

Cấp tốc 789+ thi vào lớp 10 môn Ngữ Văn

Đã bán 111

₫ 180.000 ₫ 97.000

Hà Nội

Lớp 9 - Siêu trọng tâm Toán, Văn, Anh

Đã bán 411

₫ 180.000 ₫ 97.000

Hà Nội

Cấp tốc 789+ thi vào lớp 10 môn Tiếng Anh

Đã bán 1k

₫ 180.000 ₫ 97.000

Hà Nội

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tìm tham số thực m để đồ thị hàm số y = -2x² và đường thẳng y = x - m có điểm chung.

Xem đáp án » 13/07/2024 5,782

Câu 2:

Hai vòi nước cùng chảy vào một bể cạn (không có nước) sau 40 phút thì đầy bể. Nếu mở vòi thứ nhất chảy trong 15 phút rồi khóa lại, sau đó mở vòi thứ hai chảy tiếp trong 20 phút thì lúc này lượng nước trong bể chiếm $\frac{5}{12}$ thể tích của bể nước. Hỏi nếu mở riêng từng vòi thì thời gian để mỗi vòi chảy đầy bể là bao lâu?

Xem đáp án » 13/07/2024 3,407

Câu 3:

Giải phương trình $x^{2} + 8 x + 15 = 0$

Xem đáp án » 13/07/2024 3,175

Câu 4:

Cho phương trình 3x² + 5x - 1 = 0 có hai nghiệm x₁ , x₂ . Tính giá trị biểu thức T = 6x₁ - 7x₁x₂ + 6x₂ .

Xem đáp án » 13/07/2024 2,715

Câu 5:

Rút gọn biểu thức $A = \sqrt{{(\sqrt{2} - 1)}^{2}} - \frac{1}{3} \sqrt{18}$

Xem đáp án » 13/07/2024 2,267

Câu 6:

Giải phương trình $x^{4} - 3 x^{2} - 4 = 0$

Xem đáp án » 13/07/2024 1,888

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Tìm tham số thực m để đồ thị hàm số y = -2x2 và đường thẳng y = x - m có điểm chung.

Giải phương trình x2+8x+15=0

Cho phương trình 3x2 + 5x - 1 = 0 có hai nghiệm x1 , x2 . Tính giá trị biểu thức T = 6x1 - 7x1x2 + 6x2 .

Rút gọn biểu thức A=2−12−1318

Giải phương trình x4−3x2−4=0

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Tìm tham số thực m để đồ thị hàm số y = -2x² và đường thẳng y = x - m có điểm chung.

Giải phương trình $x^{2} + 8 x + 15 = 0$

Cho phương trình 3x² + 5x - 1 = 0 có hai nghiệm x₁ , x₂ . Tính giá trị biểu thức T = 6x₁ - 7x₁x₂ + 6x₂ .

Rút gọn biểu thức $A = \sqrt{{(\sqrt{2} - 1)}^{2}} - \frac{1}{3} \sqrt{18}$

Giải phương trình $x^{4} - 3 x^{2} - 4 = 0$