Truy cập không giới hạn toàn bộ khóa học. Đăng ký ngay

✕

Kích hoạt VIP

Tạo VIP

Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 8)

58 người thi tuần này 4.6 1.3 K lượt thi 10 câu hỏi 90 phút

Đề số 1

🔥 Học sinh cũng đã học

Đề khảo sát Toán 9 năm 2026 Trường THCS Thành Công (Hà Nội) tháng 4/2026 có đáp án

0 lượt thi 9 câu hỏi

Đề thi thử vào 10 môn Toán năm 2026 Trường THCS Yên Hòa (Hà Nội) lần 3 có đáp án

0 lượt thi 9 câu hỏi

Đề thi thử vào 10 môn Toán năm 2026 Trường THCS Giảng Võ (Hà Nội) có đáp án

0 lượt thi 9 câu hỏi

Đề giao lưu vào 10 môn Toán năm 2026 THPT Ba Đình (Thanh Hóa) tháng 5/2026 có đáp án

0 lượt thi 16 câu hỏi

Đề khảo sát tuyển sinh vào 10 môn Toán năm 2026 THCS Lý Tự Trọng (Quảng Ninh) có đáp án

0 lượt thi 19 câu hỏi

Đề thi thử vào 10 môn Toán năm 2026 Phường Thái Hòa (Nghệ An) lần 3 có đáp án

0 lượt thi 11 câu hỏi

Đề thi thử vào 10 môn Toán năm 2026 TH, THCS, THPT Nobel School II (Thanh Hóa) tháng 5/2026 có đáp án

0 lượt thi 16 câu hỏi

Đề thi thử vào 10 môn Toán năm 2026 THCS Quang Thịnh (Bắc Ninh) tháng 5/2026 có đáp án

0 lượt thi 38 câu hỏi

Danh sách câu hỏi:

Câu 1/10

Giải phương trình $x^{2} + 8 x + 15 = 0$

Lời giải

$x^{2} + 8 x + 15 = 0 \Leftrightarrow x^{2} + 3 x + 5 x + 15 = 0 \Leftrightarrow (x^{2} + 3 x) + (5 x + 15) = 0 \Leftrightarrow x (x + 3) + 5 (x + 3) = 0 \Leftrightarrow (x + 3) (x + 5) = 0 \Leftrightarrow [\begin{array}{l} x + 3 = 0 \\ x + 5 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = - 3 \\ x = - 5 \end{array}$

Vậy tập nghiệm của phương trình là $S = \{- 3; - 5\} .$

Câu 2/10

Giải phương trình $x^{4} - 3 x^{2} - 4 = 0$

Lời giải

Đặt $t = x^{2} (t \geq 0)$ .

Khi đó phương trình (1) trở thành $t^{2} - 3 t - 4 = 0 (2)$ .

Ta có $a = 1; b = - 3; c = - 4$

Khi đó $Δ = b^{2} - 4 a c = {(- 3)}^{2} - 4 . 1 . (- 4) = 25 > 0 \Rightarrow \sqrt{Δ} = \sqrt{25} = 5$

Vậy phương trình (2) có hai nghiệm phân biệt

$t_{1} = \frac{- b + \sqrt{Δ}}{2 a} = \frac{3 + 5}{2} = 4$ (nhận)

$t_{2} = \frac{- b - \sqrt{Δ}}{2 a} = \frac{3 - 5}{2} = - 1$ (loại)

Với $t = t_{1} = 4$ ta có $x^{2} = 4$ . Suy ra $x_{1} = 2; x_{2} = - 2.$

Vậy tập nghiệm của phương trình (1) là S = {-2;2}

Câu 3/10

Giải hệ phương trình $\{\begin{cases} 2 x + 3 y = 13 \\ x - 3 y = 2 \end{cases}$

Lời giải

$\{\begin{cases} 2 x + 3 y = 13 \\ x - 3 y = 2 \end{cases} \Leftrightarrow \{\begin{cases} 3 x = 15 \\ x - 3 y = 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 5 \\ x - 3 y = 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 5 \\ 5 - 3 y = 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 5 \\ y = 1 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất (x;y) = (5;1)

Câu 4/10

Rút gọn biểu thức $A = \sqrt{{(\sqrt{2} - 1)}^{2}} - \frac{1}{3} \sqrt{18}$

Lời giải

$A = \sqrt{{(\sqrt{2} - 1)}^{2}} - \frac{1}{3} \sqrt{18} = \sqrt{{(\sqrt{2} - 1)}^{2}} - \frac{1}{3} \sqrt{18} = |\sqrt{2} - 1| - \frac{1}{3} \sqrt{9 . 2} = \sqrt{2} - 1 - \sqrt{2} = - 1.$

Câu 5/10

Vẽ đồ thị hàm số $y = - 2 x^{2} .$

Lời giải

Hàm số xác định với mọi $x \in ℝ$ .

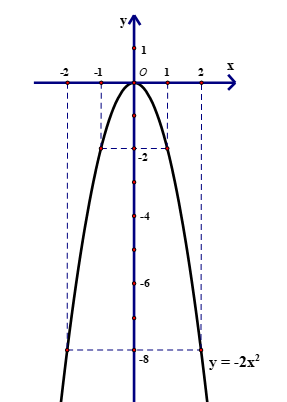
Bảng giá trị:

x	–2	–1	0	1	2
y	–8	–2	0	–2	–8

Nhận xét: Đồ thị hàm số $y = - 2 x^{2}$ là một đường cong parabol đi qua gốc tọa độ O(0;0) nhận trục Oy làm trục đối xứng, nằm phía dưới trục hoành, điểm O là điểm cao nhất của đồ thị.

Vẽ đồ thị hàm số y = -2x2 (ảnh 1)

Câu 6/10

Tìm tham số thực m để đồ thị hàm số y = -2x² và đường thẳng y = x - m có điểm chung.

Lời giải

Phương trình hoành độ giao điểm của đồ thị hàm số $y = - 2 x^{2}$ và đường thẳng $y = x - m$ là $- 2 x^{2} = x - m \Leftrightarrow 2 x^{2} + x - m = 0$

Ta có $Δ = 1^{2} - 4 . 2 . (- m) = 1 + 8 m .$

Để đồ thị hàm số $y = - 2 x^{2}$ và đường thẳng $y = x - m$ có điểm chung thì $Δ \geq 0 \Rightarrow 1 + 8 m \geq 0 \Leftrightarrow m \geq - \frac{1}{8} \cdot$

Câu 7/10

Cho phương trình 3x² + 5x - 1 = 0 có hai nghiệm x₁ , x₂ . Tính giá trị biểu thức T = 6x₁ - 7x₁x₂ + 6x₂ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8/10

Hai vòi nước cùng chảy vào một bể cạn (không có nước) sau 40 phút thì đầy bể. Nếu mở vòi thứ nhất chảy trong 15 phút rồi khóa lại, sau đó mở vòi thứ hai chảy tiếp trong 20 phút thì lúc này lượng nước trong bể chiếm $\frac{5}{12}$ thể tích của bể nước. Hỏi nếu mở riêng từng vòi thì thời gian để mỗi vòi chảy đầy bể là bao lâu?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9/10

Một hình nón có bán kính đáy r = 6cm, độ dài đường sinh l = 10cm. Tính thể tích của hình nón đó.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10/10

Cho tam giác ABC vuông tại A, trên cạnh AB lấy điểm M (M khác A, M khác B). Từ điểm M vẽ đường thẳng MN vuông góc với BC (N thuộc BC), đường thẳng MN cắt đường thẳng AC tại K.

1) Chứng minh tứ giác AMNC nội tiếp.

2) Chứng minh $\hat{A B K} = \hat{A C M} .$

3) Đoạn thẳng BKcắt đường tròn đường kính BM tại điểm D (D khác B). Gọi I là tâm và r là bán kính của đường tròn nội tiếp tam giác BKC. Chứng minh $\frac{1}{r} = \frac{1}{K N} + \frac{1}{C D} + \frac{1}{A B} \cdot$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem tiếp với tài khoản VIP

Còn 4/10 câu hỏi, đáp án và lời giải chi tiết.

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Khóa học 1 - 12

THPT

L Lớp 12 13.871 đề thi • 494 bài giảng
L Lớp 11 10.324 đề thi • 381 bài giảng
L Lớp 10 10.056 đề thi • 758 bài giảng

THCS

L Lớp 9 10.249 đề thi • 1.156 bài giảng
L Lớp 8 8.251 đề thi • 1.136 bài giảng
Xem thêm

Phòng luyện đề

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ô Ôn vào 10

Ôn vào 6

Ô Ôn vào 6

Tài liệu

THPT

THCS

Tuyển Sinh