Quảng cáo
Trả lời:
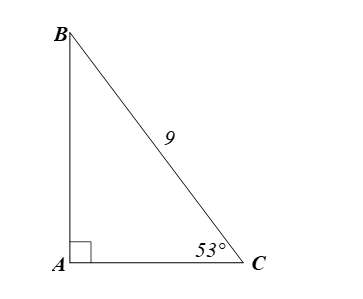
Xét ∆ABC vuông tại A, ta có: (định lí tổng ba góc của một tam giác).
Suy ra
Theo định lí 1, ta có:
⦁ AC = BC.cosC = 9.cos53° ≈ 5,416.
⦁ AB = BC.sinC = 9.sin53° ≈ 7,188.
Vậy ∆ABC có
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
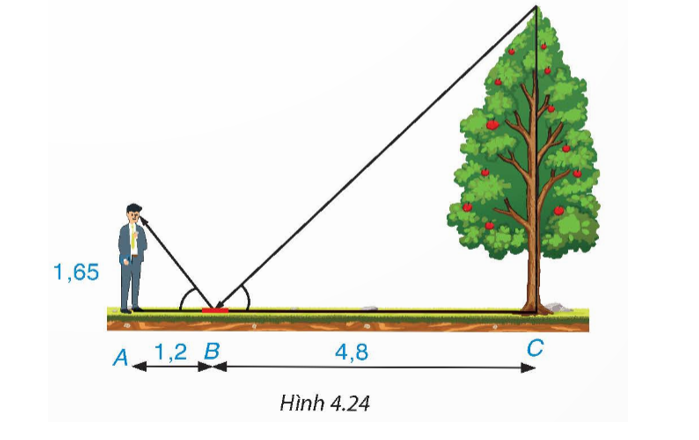
Theo đề ta có hình vẽ:
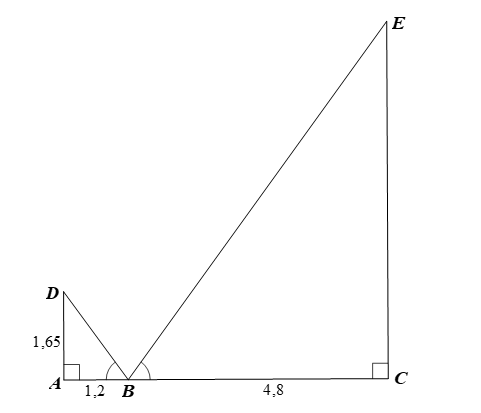
Xét ∆ABD vuông tại A, ta có
Mà nên
Xét ∆BCE vuông tại C, ta có (m).
Vậy chiều cao của cây là 6,6 m.
Lời giải
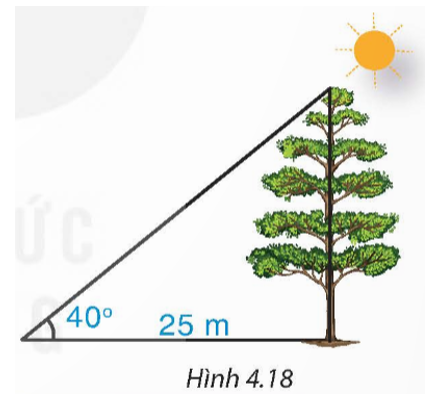
Ta nhận thấy chiều cao h của cây đối diện với góc 40° (góc tạo bởi tia nắng mặt trời và bóng của cây trên mặt đất).
Theo Định lí 2, ta có h = 25.tan40° ≈ 20,9775 (m) = 209,775 (dm) ≈ 210 (dm).
Vậy chiều cao của tháp là khoảng 210 dm.
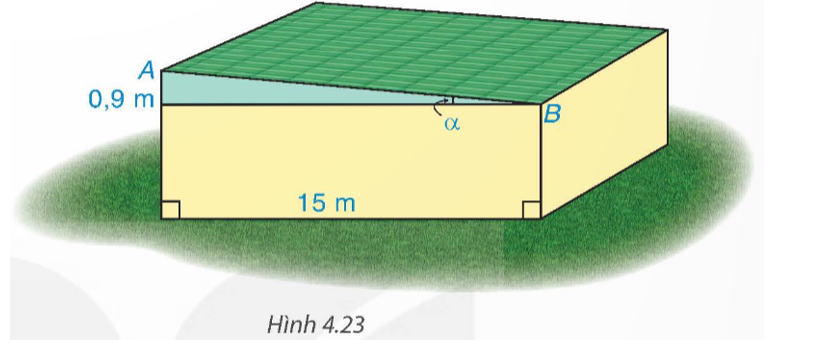
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
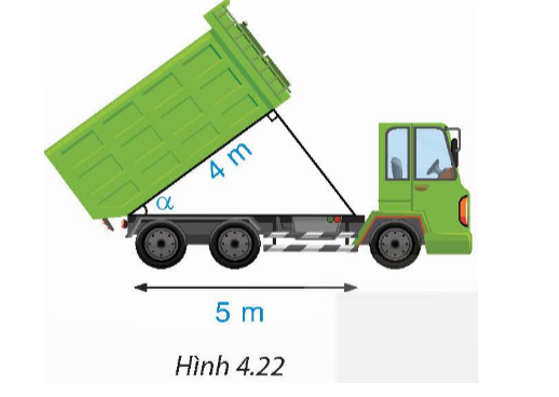
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.