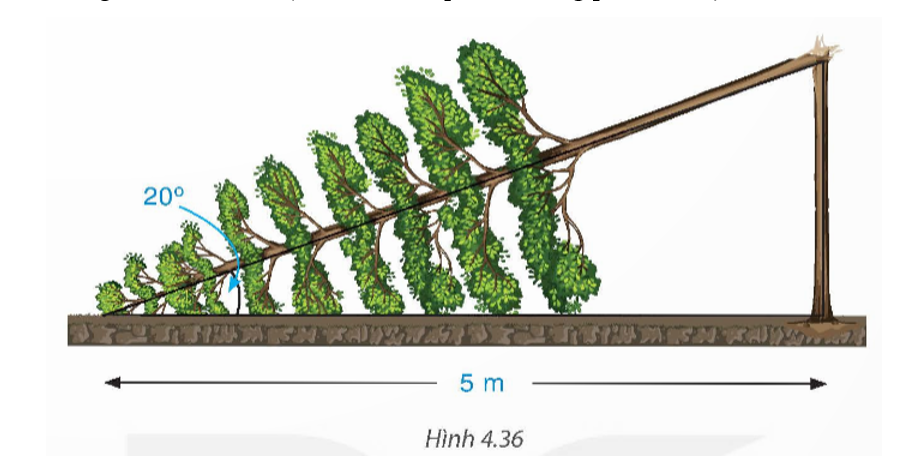
Một cây cao bị gãy, ngọn cây đổ xuống mặt đất. Ba điểm: gốc cây, điểm gãy, ngọn cây tạo thành một tam giác vuông. Đoạn cây gãy tạo với mặt đất góc 20° và chắn ngang lối đi một đoạn 5 m (H.4.36). Hỏi trước khi bị gãy, cây cao khoảng bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Câu hỏi trong đề: Giải SGK Toán 9 KNTT Bài tập cuối chương 4 có đáp án !!
Quảng cáo
Trả lời:
Giả sử hình ảnh cây bị gãy mô tả bởi hình vẽ như dưới đây
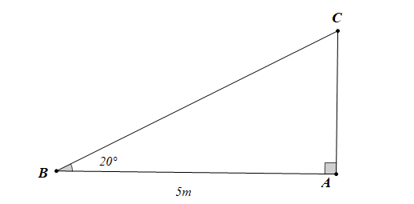
Xét ∆ABC vuông tại A, ta có:
⦁ AC = AB.tan20° = 5.tan20° ≈ 1,8 (m);
⦁ suy ra
Khi đó: AC + CB ≈ 1,8 + 5,3 = 7,1 (m).
Vậy trước khi bị gãy, cây cao khoảng 7,1 m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
Với mọi góc nhọn α, ta có:
⦁ sin(90° – α) = cosα;
⦁ tan(90° – α) = cotα;
⦁ cot(90° – α) = tanα.
Vậy ta chọn phương án A.
Lời giải
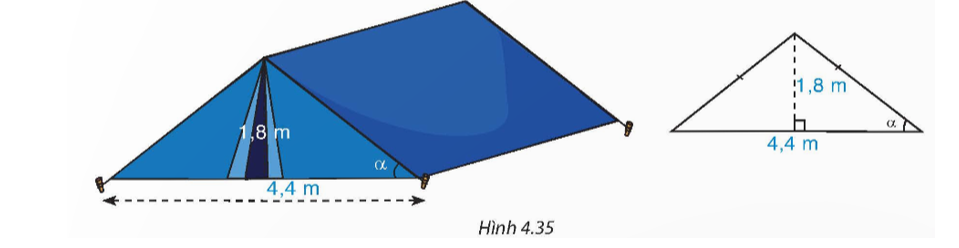
Ta có: suy ra α ≈ 39°17’.
Vậy góc α giữa cạnh mái lều và mặt đất là khoảng 39°17’.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Thanh Tam Pham
hay á