Câu hỏi:
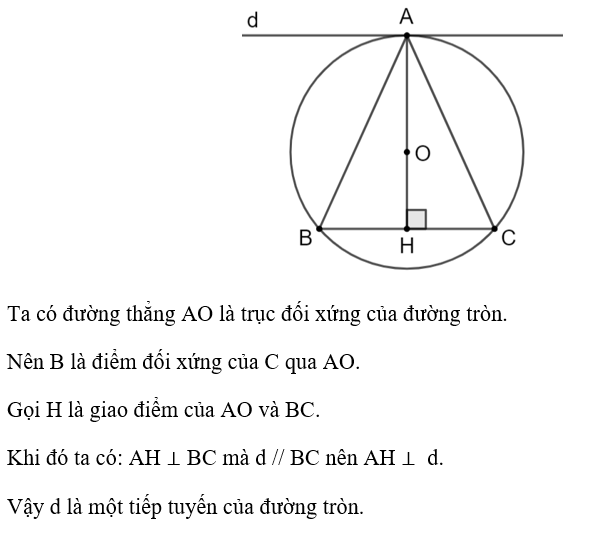
13/07/2024 4,884Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F.
a) Chứng minh rằng chu vi của tam giác SEF bằng SA + SB.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a)
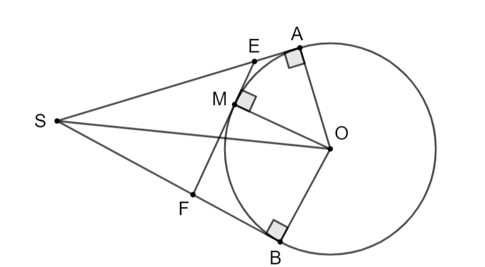
Hai tiếp tuyến EM và EA cắt nhau tại E nên EM = EA.
Hai tiếp tuyến FM và EB cắt nhau tại F nên FM = FB.
Chu vi tam giác SEF là:
CSEF = SE + SF + EF = SE + SF + EM + MF
= SE + EA + SF + BF = SA + SB.
Vậy chu vi của tam giác SEF bằng SA + SB.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
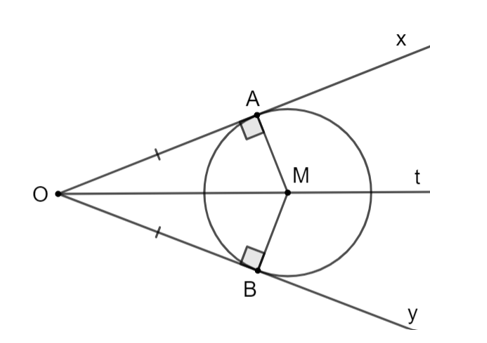
Xét ΔOAM và ΔOBM có:
OM chung
(do OM là tia phân giác của góc )
OA = OB
Do đó ΔOAM = ΔOBM (c.g.c).
Suy ra AM = BM (hai cạnh tương ứng).
Và (hai góc tương ứng) hay OB ⊥ MB.
Do đó OA là tiếp tuyến của đường tròn (M; MA).
Vậy OA và OB là hai tiếp tuyến cắt nhau của (O).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 1. Phương trình quy về phương trình bậc nhất một ẩn có đáp án
Nhắn tin Zalo