Trong không gian Oxyz, cho hai mặt phẳng (P): x + 3y + z + 2 = 0 và (Q): x + 3y + z + 5 = 0.

a) Chứng minh rằng (P) và (Q) song song với nhau.

b) Lấy một điểm thuộc (P), tính khoảng cách từ điểm đó đến (Q). Từ đó tính khoảng cách giữa hai mặt phẳng (P) và (Q).

Xem lời giải

Câu hỏi trong đề: Giải SGK Toán 12 KNTT Bài 14. Phương trình mặt phẳng có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Ta có \(\overrightarrow {{n_P}} = \left( {1;3;1} \right),\overrightarrow {{n_Q}} = \left( {1;3;1} \right)\).

Vì \(\overrightarrow {{n_P}} = \overrightarrow {{n_Q}} \) và 2 ≠ 5. Do đó (P) và (Q) song song với nhau.

b) Lấy điểm M(0; 0; −2) ∈ (P).

Khi đó khoảng cách từ M đến mặt phẳng (Q) là:

\(d\left( {M,\left( Q \right)} \right) = \frac{{\left| { - 2 + 5} \right|}}{{\sqrt {1 + {3^2} + 1} }} = \frac{3}{{\sqrt {11} }}\).

Do đó \(d\left( {M,\left( Q \right)} \right) = d\left( {\left( P \right),\left( Q \right)} \right) = \frac{3}{{\sqrt {11} }}\).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian Oxyz, viết phương trình mặt phẳng đi qua M(2; 3; −1), song song với trục Ox và vuông góc với mặt phẳng (Q): x + 2y – 3z + 1 = 0.

Xem đáp án

Lời giải

Gọi mặt phẳng cần tìm là mặt phẳng (P).

Ta có \(\overrightarrow i = \left( {1;0;0} \right)\) và \(\overrightarrow {{n_Q}} = \left( {1;2; - 3} \right)\).

Vì (P) // Ox và (P) ^ (Q) nên \(\overrightarrow {{n_P}} = \left[ {\overrightarrow i ,\overrightarrow {{n_Q}} } \right] = \left( {0;3;2} \right)\).

Mặt phẳng đi qua M(2; 3; −1) và nhận \(\overrightarrow {{n_P}} = \left( {0;3;2} \right)\) làm một vectơ pháp tuyến có phương trình là: 3(y – 3) + 2(z + 1) = 0 Û 3y + 2z – 7 = 0.

Câu 2

(H.5.14) Góc quan sát ngang của một camera là 115°. Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 4) và chiếu thẳng về phía mặt phẳng (P): x + 2y + 2z + 3 = 0. Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có bán kính bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất)

Xem đáp án

Lời giải

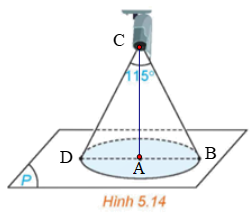
(H.5.14) Góc quan sát ngang của một camera là 115°. Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 4) và chiếu thẳng về phía mặt phẳng (P): x + 2y + 2z + 3 = 0. Hỏi vùng quan sát được trên mặt phẳng (ảnh 2)

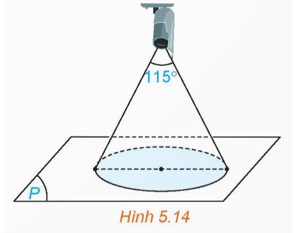
Chọn các điểm như hình vẽ.

Gọi A là hình chiếu của C trên mặt phẳng (P).

Vì CBD là tam giác cân nên CA là đường cao, phân giác, trung tuyến của BD.

Ta có \(CA = d\left( {C,\left( P \right)} \right) = \frac{{\left| {1 + 2.2 + 2.4 + 3} \right|}}{{\sqrt {1 + {2^2} + {2^2}} }} = \frac{{16}}{3}\).

Vì tam giác CAB vuông tại A, có \(\widehat {ACB} = \frac{{115^\circ }}{2} = 57,5^\circ \).

Suy ra R = AB = CA.tan57,5° ≈ 8,4.

Vậy vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có bán kính bằng 8,4.

Câu 3