Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3 cm. Tính diện tích tam giác ABC.
Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3 cm. Tính diện tích tam giác ABC.
Quảng cáo
Trả lời:
Giải bởi Vietjack
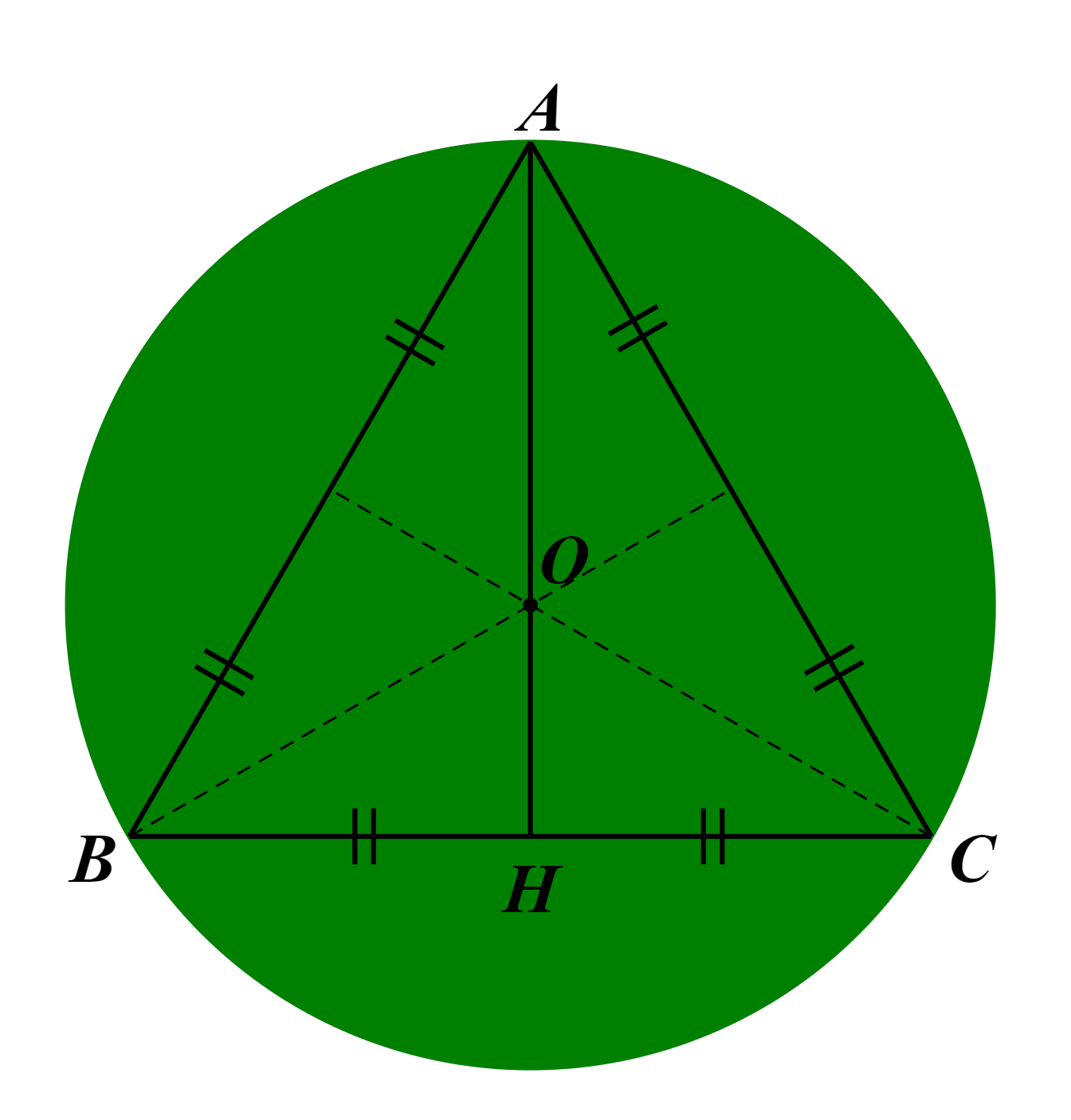
Vì tam giác ABC đều nên tâm O của đường tròn ngoại tiếp tam giác là trọng tâm của tam giác đó và bán kính đường tròn ngoại tiếp tam giác là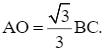 
Theo bài, AO = 3 cm nên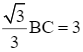 
Suy ra 
Gọi H là giao điểm của AO và BC. Khi đó AH vừa là đường trung trực, vừa là đường trung tuyến, cũng là đường cao của tam giác.
Ta có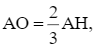 
suy ra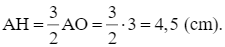 
Diện tích của tam giác ABC là:
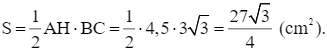
Vậy diện tích của tam giác ABC là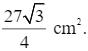 
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi độ dài các cạnh phía bên trong của khung gỗ là a (cm).
Bán kính của chiếc đồng hồ hình tròn là: r = 30 : 2 = 15 (cm).
Vì khung gỗ hình tam giác đều để đặt vừa khít chiếc đồng hồ nên đường tròn khung viền của đồng hồ nội tiếp tam giác chứa cạnh của khung gỗ và bán kính đường tròn này là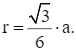 
Suy ra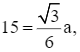 
suy ra 
Vậy độ dài cạnh của tam giác (phía bên trong) của khung gỗ là 
Lời giải
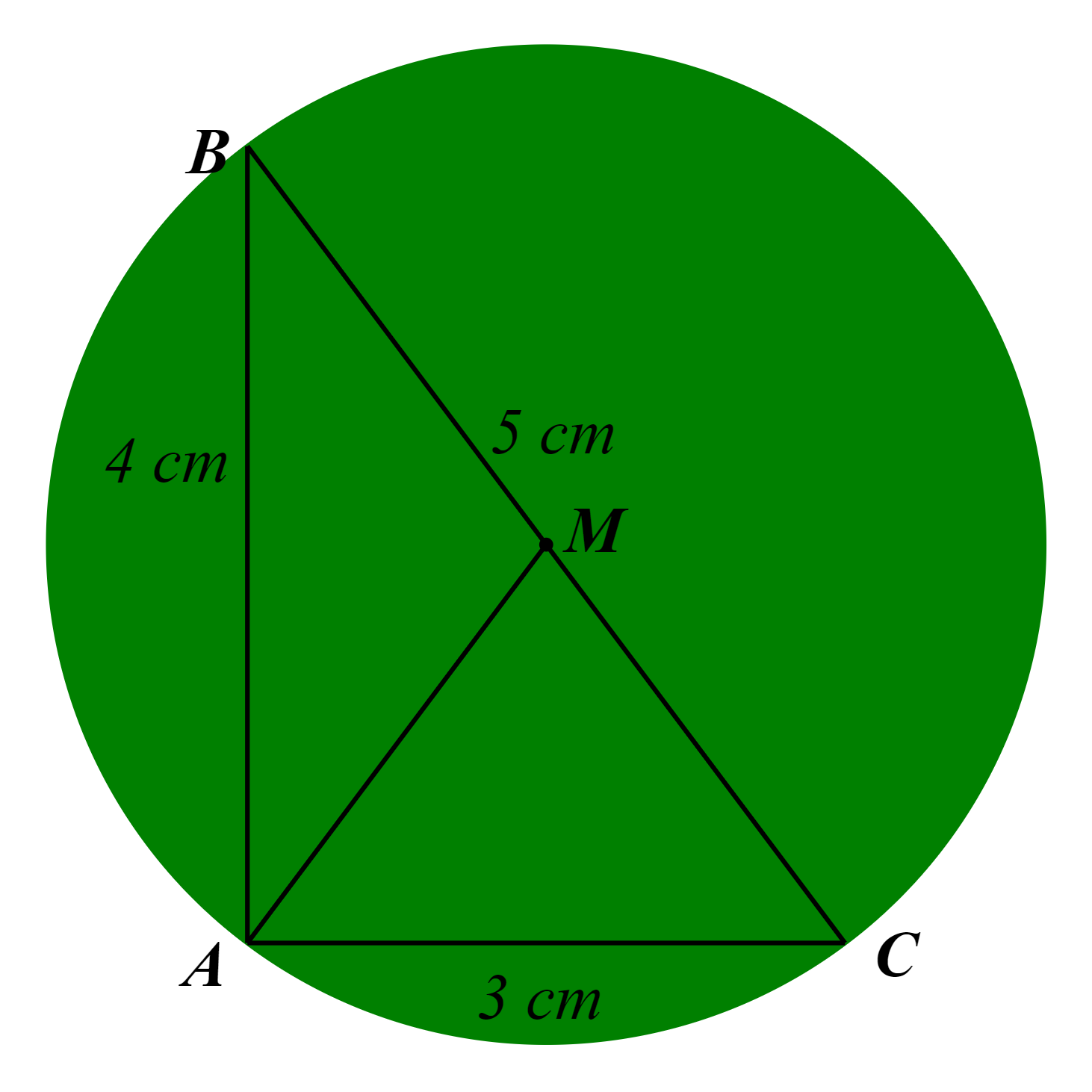
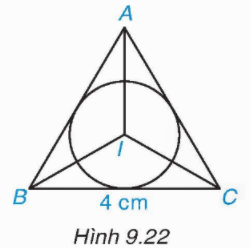
Xét ∆ABC có:
⦁ AB2 + AC2 = 42 + 32 = 25;
⦁ BC2 = 52 = 25.
Do đó AB2 + AC2 = BC2.
Suy ra tam giác ABC vuông tại A (định lí Pythagore đảo).
Theo kết quả của Hoạt động 3, trang 73, SGK Toán 9, Tập 2, ta có tâm đường tròn ngoại tiếp ∆ABC là trung điểm M của BC và bán kính của đường tròn ngoại tiếp ∆ABC là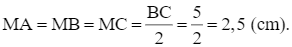 
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo