Câu hỏi:
13/07/2024 216
Cầu Trường Tiền (hay cầu Tràng Tiền) ở thành phố Huế được khởi công vào tháng 5/1899 và khánh thành vào ngày 18/12/1900. Cầu được thiết kế theo kiến trúc Gothic, bắc qua sông Hương. Từ Festival Huế năm 2002, cầu Trường Tiền được lắp đặt một hệ thống chiếu sáng đổi màu hiện đại. Cầu dài 402,60 m, gồm 6 nhịp dầm thép.
(Nguồn: https://vi.wikipedia.org)
Giả sử một nhịp dầm thép có dạng parabol y = ax2 trong hệ trục toạ độ Oxy, ở đó Ox song song với mặt cầu. Biết rằng, hai chân nhịp dầm thép trên mặt cầu cách nhau 66,66 m, khoảng cách từ đỉnh cao nhất của nhịp dầm thép đến mặt cầu là 5,45 m (Hình 11).
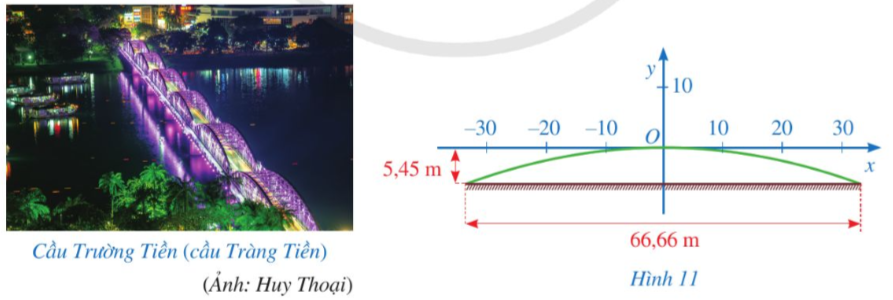
Tìm a (làm tròn kết quả đến hàng phần nghìn).
Cầu Trường Tiền (hay cầu Tràng Tiền) ở thành phố Huế được khởi công vào tháng 5/1899 và khánh thành vào ngày 18/12/1900. Cầu được thiết kế theo kiến trúc Gothic, bắc qua sông Hương. Từ Festival Huế năm 2002, cầu Trường Tiền được lắp đặt một hệ thống chiếu sáng đổi màu hiện đại. Cầu dài 402,60 m, gồm 6 nhịp dầm thép.
(Nguồn: https://vi.wikipedia.org)
Giả sử một nhịp dầm thép có dạng parabol y = ax2 trong hệ trục toạ độ Oxy, ở đó Ox song song với mặt cầu. Biết rằng, hai chân nhịp dầm thép trên mặt cầu cách nhau 66,66 m, khoảng cách từ đỉnh cao nhất của nhịp dầm thép đến mặt cầu là 5,45 m (Hình 11).
Câu hỏi trong đề: Giải SGK Toán 9 CD Bài tập cuối chương 7 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì đồ thị hàm số y = ax2 đi qua điểm B(33,33; –5,45) nên thay x = 33,33 và y = –5,45 vào hàm số y = ax2, ta được:
–5,45 = a.33,332, suy ra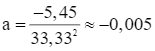 
(thỏa mãn).
Vậy a ≈ –0,005.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Giá của chiếc áo sau lần giảm giá thứ nhất là:
120 000 – 120 000 . x% = 120 000 – 1 200x (đồng).
Giá của chiếc áo sau hai lần giảm giá là:
120 000 – 1 200x – (120 000 – 1 200x).x%
= 120 000 – 1 200x – 1 200x + 12x2
= 12x2 – 2 400x + 120 000 (đồng).
Theo bài, sau hai đợt giảm giá, giá của chiếc áo còn 76 800 đồng nên ta có phương trình:
12x2 – 2 400x + 120 000 = 76 800
12x2 – 2 400x + 43 200 = 0
x2 – 200x + 3 600 = 0.
Phương trình trên có các hệ số a = 1, b = –200, c = 3 600.
Do b = –200 nên b’ = –100.
Ta có: ∆’ = (–100)2 – 1 . 3 600 = 6 400 > 0.
Do ∆’ > 0 nên phương trình trên có hai nghiệm phân biệt là:
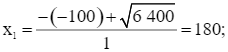
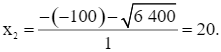
Ta thấy chỉ có giá trị x2 = 20 thỏa mãn điều kiện vì x% < 100%.
Vậy x = 20 là giá trị cần tìm.
Lời giải
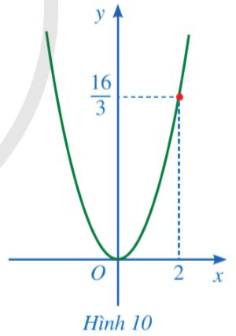
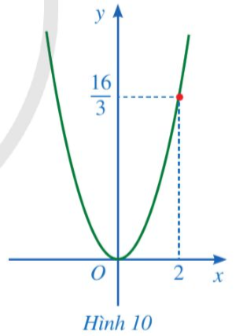
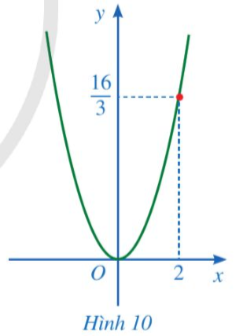
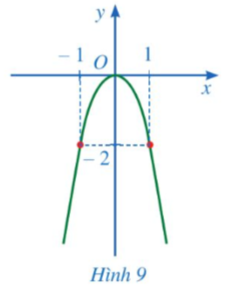
Điểm thuộc đồ thị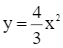 
có tung độ bằng 4 nên thay y = 4 vào hàm số 
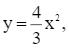ta được: 
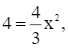suy ra 
nên 
hoặc 
Vậy các điểm cần tìm là 
và 
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận