Tại một nhà máy sản xuất một loại phân bón, gọi P(x) là lợi nhuận (tính theo triệu đồng) thu được từ việc bán x tấn sản phẩm trong một tuần. Khi đó, đạo hàm P'(x), gọi là lợi nhuận cận biên, cho biết tốc độ tăng lợi nhuận theo lượng sản phẩn bán được. Giả sử lợi nhuận cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức P'(x) = 16 – 0,02x với 0 ≤ x ≤ 100. Tính lợi nhuận nhà máy thu được khi bán 90 tấn sản phẩm trong tuần. Biết rằng nhà máy lỗ 25 triệu đồng nếu không bán được lượng sản phẩm nào trong tuần.
Tại một nhà máy sản xuất một loại phân bón, gọi P(x) là lợi nhuận (tính theo triệu đồng) thu được từ việc bán x tấn sản phẩm trong một tuần. Khi đó, đạo hàm P'(x), gọi là lợi nhuận cận biên, cho biết tốc độ tăng lợi nhuận theo lượng sản phẩn bán được. Giả sử lợi nhuận cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức P'(x) = 16 – 0,02x với 0 ≤ x ≤ 100. Tính lợi nhuận nhà máy thu được khi bán 90 tấn sản phẩm trong tuần. Biết rằng nhà máy lỗ 25 triệu đồng nếu không bán được lượng sản phẩm nào trong tuần.
Câu hỏi trong đề: Giải SGK Toán 12 CTST Bài 2. Tích phân có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lợi nhuận nhà máy thu được khi bán x sản phẩm trong tuần là:
\(P\left( x \right) = \int {\left( {16 - 0,02x} \right)dx} \) \( = 16x - 0,01{x^2} + C\)
Vì P(0) = −25 nên 16.0 – 0,01.02 + C = −25 Þ C = −25.
Do đó P(x) = −0,01x2 + 16x – 25.
Lợi nhuận nhà máy thu được khi bán 90 tấn sản phẩm trong tuần là:
P(90) = −0,01.902 + 16.90 – 25 = 1334 triệu đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Sau khi học xong bài này, ta giải quyết bài toán này như sau:
Xe dừng khi v(t) = 20 – 5t = 0 Û t = 4.
Quãng đường xe di chuyển từ khi bắt đầu hãm phanh đến khi dừng là:
(m).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
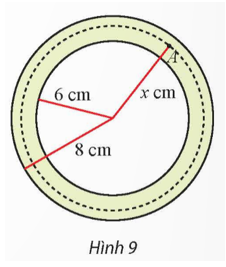
Nhiệt độ tại điểm A trên thành ống là
\(T\left( x \right) = \int { - \frac{{30}}{x}} dx = - 30\ln \left| x \right| + C\).
Vì T(6) = 150°C nên −30ln6 + C = 150 Þ C = 150 + 30ln6.
Do đó T(x) = −30ln|x| + 150 + 30ln6.
Nhiệt độ ngoài mặt ống là T(8) = −30ln8 + 150 + 30ln6 ≈ 141,37°C.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập