Quảng cáo
Trả lời:
Gọi x, y lần lượt là số lít nước sinh tố loại thứ nhất và loại thứ hai mà công ty dự định sản xuất.
Tổng số tiền công ty thu được khi bán x lít nước sinh tố loại thứ nhất và y lít nước sinh tố loại thứ hai là: T = 24 000x + 18 000y (đồng).
Số lít nước anh đào có trong x lít nước sinh tố loại thứ nhất và y lít nước sinh tố loại thứ hai là 0,7x + 0,4y (lít).
Số lít nước cam có trong x lít nước sinh tố loại thứ nhất và y lít nước sinh tố loại thứ hai là 0,3x + 0,6y (lít).
Vì lượng nguyên liệu sử dụng không vượt quá lượng dự trữ nên ta có thể viết dạng tổng quát của bài toán quy hoạch tuyến tính sau:
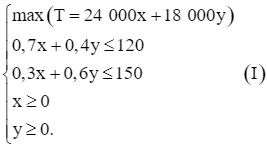
Xét hệ bất phương trình bậc nhất hai ẩn (x, y là các số thực):
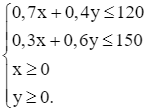 hay
hay 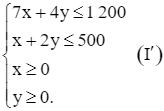
Ta cần tìm giá trị lớn nhất của biểu thức T = 24 000x + 18 000y khi (x; y) thỏa mãn hệ bất phương trình (I’).
Bước 1. Xác định miền nghiệm của hệ bất phương trình (I’).
Miền nghiệm là miền tứ giác OABC với tọa độ các đỉnh O(0; 0), A(0; 250), B(40; 230), 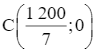 (hình vẽ).
(hình vẽ).
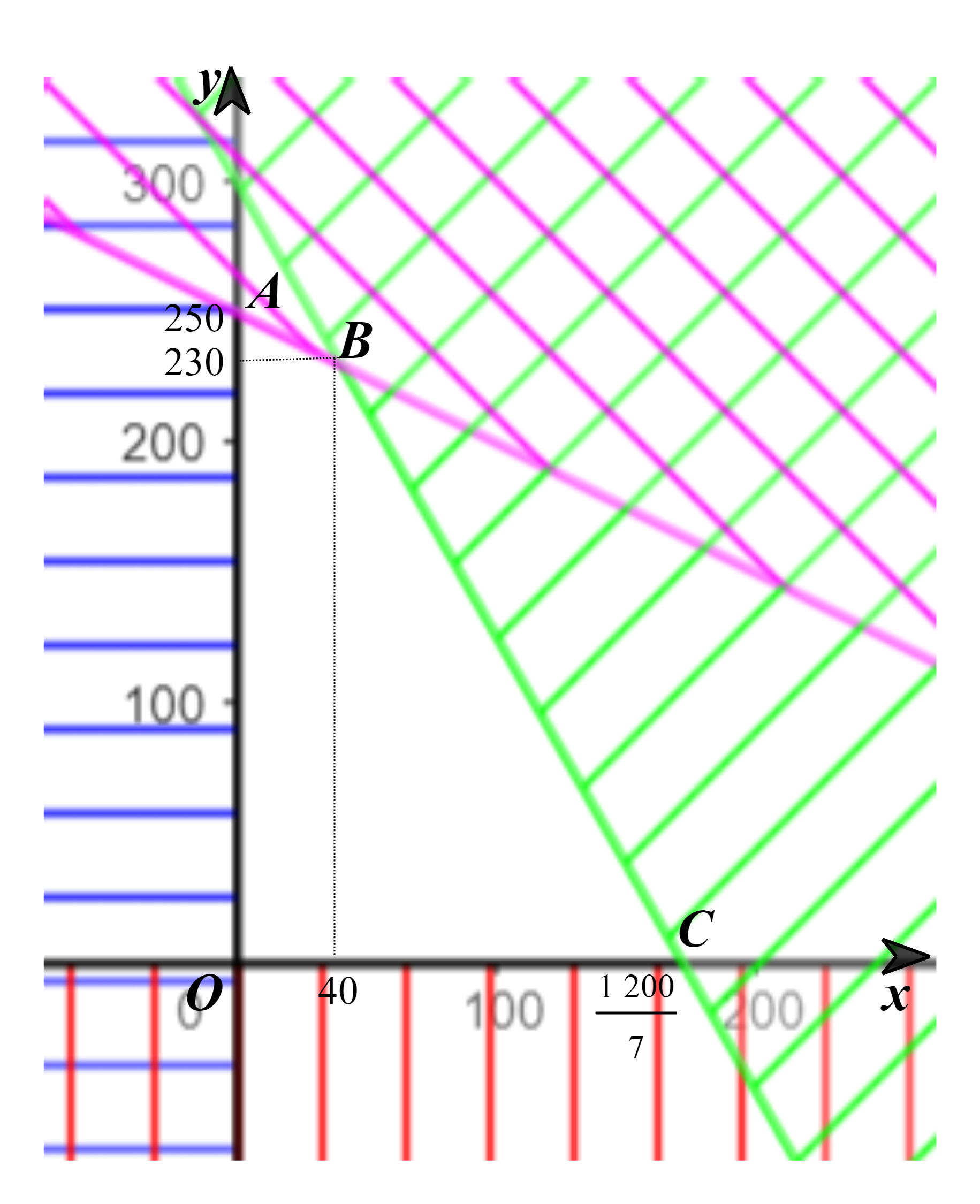
Bước 2. Tính giá trị của biểu thức T(x; y) = 24 000x + 18 000y tại các đỉnh của tứ giác này:
T(0; 0) = 0; T(0; 250) = 4 500 000; T(40; 230) = 5 100 000;
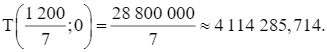
Bước 3. Ta đã biết biểu thức T = 24 000x + 18 000y đạt giá trị lớn nhất tại cặp số thực (x; y) là tọa độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của T ở Bước 2, ta được giá trị lớn nhất cần tìm là T(40; 230) = 5 100 000.
Bước 4. Vì 40 và 230 đều là số tự nhiên nên cặp số (x; y) = (40; 230) là nghiệm của bài toán (I).
Vậy công ty phải sản xuất 40 lít nước sinh tố loại thứ nhất và 230 lít sinh tố loại thứ hai để tổng số tiền công ty thu được là nhiều nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x và y lần lượt là số sản phẩm loại A và loại B người đó cần sơn (x ∈ ℕ, y ∈ ℕ).
Số tiền lãi người đó thu được là: T = 10x + 8y (triệu đồng).
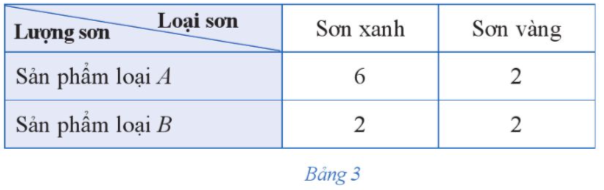
Số kg sơn xanh người đó cần dùng là: 6x + 2y ≤ 12 hay 3x + y ≤ 6;
Số kg sơn vàng người đó cần dùng là: 2x + 2y ≤ 8 hay x + y ≤ 4.
Vì vậy, yêu cầu của người đó có thể viết ở dạng tổng quát của bài toán quy hoạch tuyến tính sau:
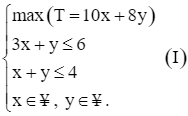
Xét hệ bất phương trình bậc nhất hai ẩn (x, y là các số thực): 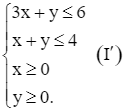
Ta cần tìm giá trị lớn nhất của biểu thức T = 10x + 8y khi (x; y) thỏa mãn hệ bất phương trình (I’).
Bước 1. Xác định miền nghiệm của hệ bất phương trình (I’).
Miền nghiệm là miền tứ giác OABC với tọa độ các đỉnh O(0; 0), A(0; 4), B(1; 3), C(2; 0) (hình vẽ).
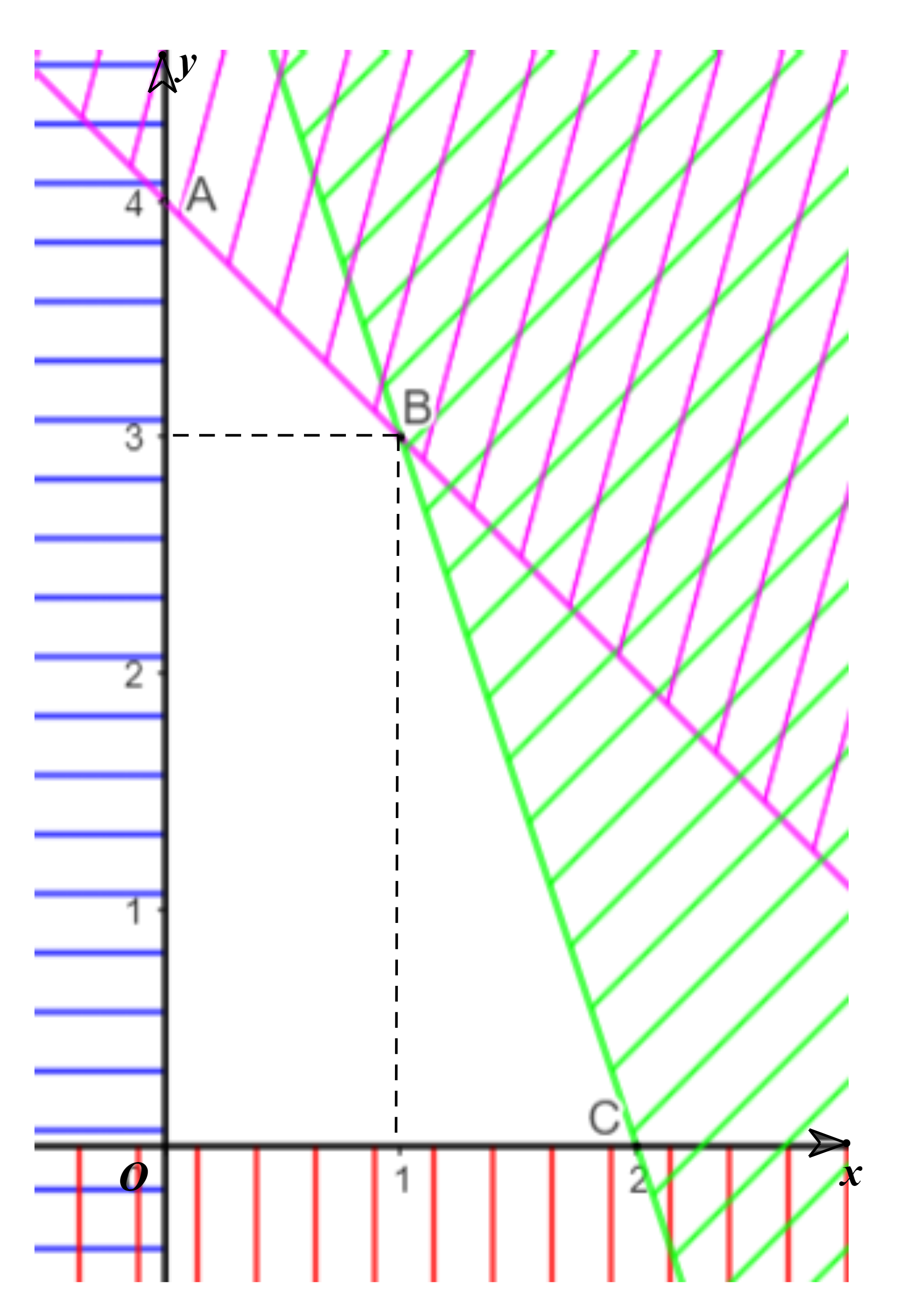
Bước 2. Tính giá trị của biểu thức T(x; y) = 10x + 8y tại các đỉnh của tứ giác này:
T(0; 0) = 0; T(0; 4) = 32; T(1; 3) = 34; T(2; 0) = 20.
Bước 3. Ta đã biết biểu thức T = 10x + 8y đạt giá trị lớn nhất tại cặp số thực (x; y) là tọa độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của T ở Bước 2, ta được giá trị lớn nhất cần tìm là T(1; 3) = 34.
Bước 4. Vì 1 và 3 đều là các số tự nhiên nên cặp số (1; 3) là nghiệm của bài toán (I).
Vậy để số tiền lãi thu được là lớn nhất thì cần sơn 1 sản phẩm loại A và 3 sản phẩm loại B.
Lời giải
Đổi 40 triệu đồng = 40 000 nghìn đồng.
Gọi x là số chiếc bàn và y là số chiếc tủ cần sản xuất (x ∈ ℕ, y ∈ ℕ).
Số ghế cần sản xuất là: 6x (chiếc).
Tổng doanh thu đạt được là: T = 260.x + 120.6x + 600.y = 980x + 600y (nghìn đồng).
Công lao động để sản xuất các loại sản phẩm trên là:
2x + 1.6x + 3y ≤ 500 hay 8x + 3y ≤ 500.
Chi phí sản xuất các loại sản phẩm trên là:
100x + 40.6x + 250y ≤ 40 000 hay 34x + 25y ≤ 4 000.
Vì vậy, yêu cầu của cơ sở sản xuất có thể viết ở dạng tổng quát của bài toán quy hoạch tuyến tính sau:
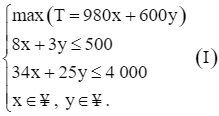
Xét hệ bất phương trình bậc nhất hai ẩn (x, y là các số thực): 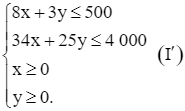
Ta cần tìm giá trị lớn nhất của biểu thức T = 980x + 600y khi (x; y) thỏa mãn hệ bất phương trình (I’).
Bước 1. Xác định miền nghiệm của hệ bất phương trình (I’).
Miền nghiệm là miền tứ giác OABC với tọa độ các đỉnh O(0; 0), A(0; 160), 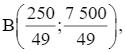 C(62,5; 0) (hình vẽ).
C(62,5; 0) (hình vẽ).
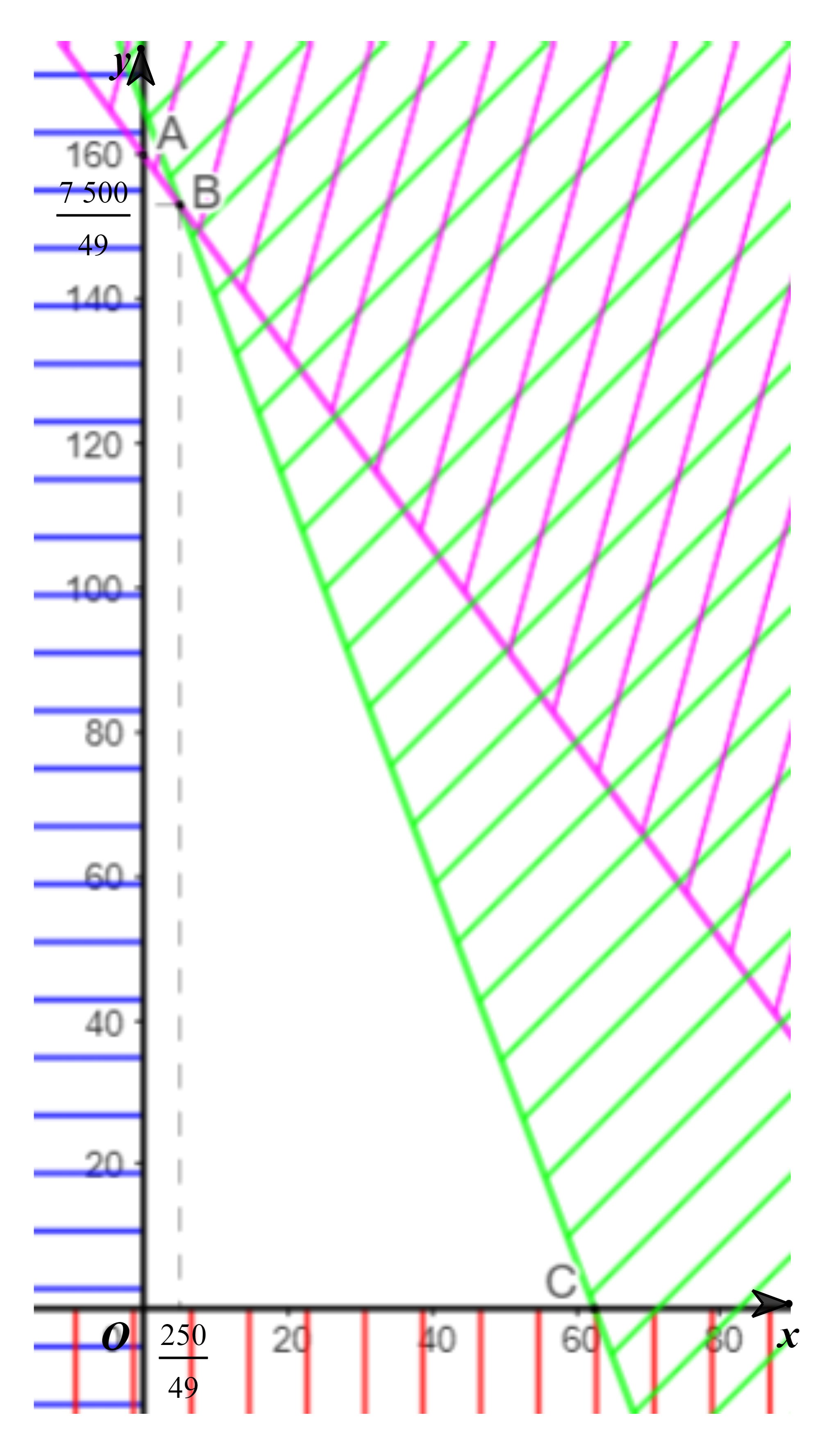
Bước 2. Tính giá trị của biểu thức T(x; y) = 980x + 600y tại các đỉnh của tứ giác này:
T(0; 0) = 0; T(0; 160) = 96 000; 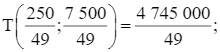 T(62,5; 0) = 61 250.
T(62,5; 0) = 61 250.
Bước 3. Ta đã biết biểu thức T = 980x + 600y đạt giá trị lớn nhất tại cặp số thực (x; y) là tọa độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của T ở Bước 2, kết hợp điều kiện x và y là các số tự nhiên, ta được giá trị lớn nhất cần tìm là T(0; 160) = 96 000.
Vậy chỉ cần sản xuất 160 chiếc tủ để tổng doanh thu đạt được cao nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.