Câu hỏi:
13/07/2024 32,910
Cho hàm số y = f(x). Đồ thị của đạo hàm y = f'(x) là đường cong trong Hình 2. Biết rằng diện tích của các phần hình phẳng A và B lần lượt là SA = 2 và SB = 3. Nếu f(0) = 4 thì f(5) bằng
A. 3.
B. 5.
C. 9.
D. −1.
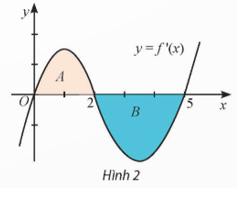
Cho hàm số y = f(x). Đồ thị của đạo hàm y = f'(x) là đường cong trong Hình 2. Biết rằng diện tích của các phần hình phẳng A và B lần lượt là SA = 2 và SB = 3. Nếu f(0) = 4 thì f(5) bằng
A. 3.
B. 5.
C. 9.
D. −1.
Câu hỏi trong đề: Giải SGK Toán 12 CTST Bài tập cuối chương 4 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Có \[{S_A} = \int\limits_0^2 {f'\left( x \right)dx = \left. {f\left( x \right)} \right|} _0^2 = f\left( 2 \right) - f\left( 0 \right) = 2 \Rightarrow f\left( 2 \right) = 2 + f\left( 0 \right) = 6\].
Mà \({S_B} = \int\limits_2^5 {\left| {f'\left( x \right)} \right|dx} = - \int\limits_2^5 {f'\left( x \right)dx} = - \left[ {f\left( 5 \right) - f\left( 2 \right)} \right] = 3\)Þ f(5) = f(2) – 3 = 6 – 3 = 3.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
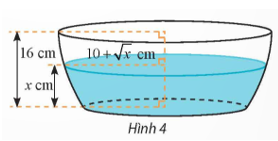
Diện tích của mặt cắt là: \(S\left( x \right) = \pi {\left( {10 + \sqrt x } \right)^2}\).
Dung tích của chậu là:
\(V = \int\limits_0^{16} {S\left( x \right)dx} = \pi \int\limits_0^{16} {{{\left( {10 + \sqrt x } \right)}^2}dx} \) \( = \pi \int\limits_0^{16} {\left( {100 + 20\sqrt x + x} \right)dx} \)
\( = \pi \left. {\left( {100x + \frac{{40}}{3}{x^{\frac{3}{2}}} + \frac{{{x^2}}}{2}} \right)} \right|_0^{16}\)\( = \frac{{7744}}{3}\pi \).
Lời giải
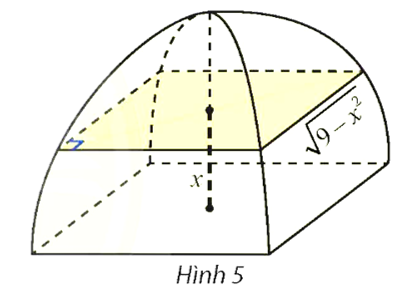
Diện tích mặt cắt là: \(S\left( x \right) = \left( {9 - {x^2}} \right)\) (m2).
Thể tích của lều là: \(V = \int\limits_0^3 {\left( {9 - {x^2}} \right)dx} \)\( = \left. {\left( {9x - \frac{{{x^3}}}{3}} \right)} \right|_0^3\)= 18.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận