Câu hỏi:
11/07/2024 7,310
Trên một cánh đồng điện mặt trời, người ta đã thiết lập sẵn một hệ tọa độ Oxyz. Hai tấm pin năng lượng lần lượt nằm trong hai mặt phẳng (P): 2x + 2z + 1 = 0 và (P'): x + z + 7 = 0.
a) Tính góc giữa (P) và (P').
b) Tính góc hợp bởi (P) và (P') với mặt đất (Q) có phương trình z = 0.
Trên một cánh đồng điện mặt trời, người ta đã thiết lập sẵn một hệ tọa độ Oxyz. Hai tấm pin năng lượng lần lượt nằm trong hai mặt phẳng (P): 2x + 2z + 1 = 0 và (P'): x + z + 7 = 0.
a) Tính góc giữa (P) và (P').
b) Tính góc hợp bởi (P) và (P') với mặt đất (Q) có phương trình z = 0.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Mặt phẳng (P) có vectơ pháp tuyến là \(\overrightarrow n = \left( {2;0;2} \right)\).
Mặt phẳng (P') có vectơ pháp tuyến là \(\overrightarrow {n'} = \left( {1;0;1} \right)\).
\(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \frac{{\left| {2.1 + 0.0 + 2.1} \right|}}{{\sqrt {{2^2} + {2^2}} .\sqrt {{1^2} + {1^2}} }} = \frac{4}{4} = 1\).
Suy ra ((P), (P')) = 0°.
b) Mặt phẳng (Q) có vectơ pháp tuyến là \(\overrightarrow {{n_Q}} = \left( {0;0;1} \right)\).
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \frac{{\left| {2.0 + 0.0 + 2.1} \right|}}{{\sqrt {{2^2} + {2^2}} .\sqrt {{1^2}} }} = \frac{2}{{2\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\).
Suy ra ((P), (Q)) = 45°.
\(\cos \left( {\left( {P'} \right),\left( Q \right)} \right) = \frac{{\left| {1.0 + 0.0 + 1.1} \right|}}{{\sqrt {{1^2} + {1^2}} .\sqrt 1 }} = \frac{1}{{\sqrt 2 }}\).
Suy ra ((P'), (Q)) = 45°.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
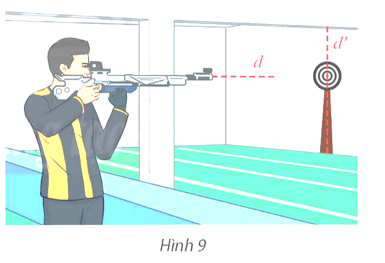
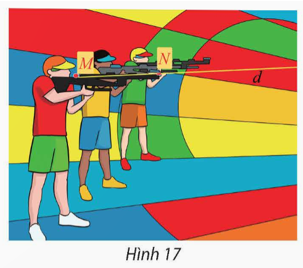
Đường thẳng d và d' lần lượt có vectơ chỉ phương là \(\overrightarrow a = \left( {1;0;0} \right),\overrightarrow {a'} = \left( {0;0;3} \right)\).
Ta có \(\overrightarrow a .\overrightarrow {a'} \) = 1.0 + 0.0 + 0.3 = 0.
Do đó d và d' vuông góc với nhau.
Lời giải
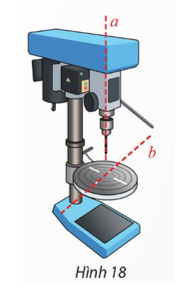
a) Đường thẳng a đi qua M(1; 2; 0) và có vectơ chỉ phương là \(\overrightarrow a = \left( {0;0;3} \right)\).
Đường thẳng b đi qua N(1; 2; 6) và có vectơ chỉ phương \(\overrightarrow {a'} = \left( {4;2;0} \right)\).
Có \(\overrightarrow a .\overrightarrow {a'} = 0.4 + 0.2 + 3.0 = 0\). Suy ra a ^ b.
Ta xét hệ \(\left\{ \begin{array}{l}1 = 1 + 4t'\\2 = 2 + 2t'\\3t = 6\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}t' = 0\\t' = 0\\t = 2\end{array} \right.\) . Suy ra hệ có nghiệm duy nhất.
Do đó a và b cắt nhau.
b) Thay t = 2 vào phương trình đường thẳng a ta được \(\left\{ \begin{array}{l}x = 1\\y = 2\\z = 6\end{array} \right.\).
Vậy tọa độ giao điểm của hai đường thẳng này là (1; 2; 6).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận