Cho hai mặt phẳng (P): x – y – 6 = 0 và (Q). Biết rằng điểm H(2; −1; −2) là hình chiếu vuông góc của gốc tọa độ O(0; 0; 0) xuống mặt phẳng (Q). Tính góc giữa mặt phẳng (P) và mặt phẳng (Q).
Cho hai mặt phẳng (P): x – y – 6 = 0 và (Q). Biết rằng điểm H(2; −1; −2) là hình chiếu vuông góc của gốc tọa độ O(0; 0; 0) xuống mặt phẳng (Q). Tính góc giữa mặt phẳng (P) và mặt phẳng (Q).
Câu hỏi trong đề: Giải SGK Toán 12 CTST Bài tập cuối chương 5 có đáp án !!
Quảng cáo
Trả lời:
Vì điểm H(2; −1; −2) là hình chiếu vuông góc của gốc tọa độ O(0; 0; 0) xuống mặt phẳng (Q) nên mặt phẳng (Q) nhận \(\overrightarrow {OH} = \left( {2; - 1; - 2} \right)\) làm một vectơ pháp tuyến.
Mặt phẳng (P) có một vectơ pháp tuyến là \(\overrightarrow n = \left( {1; - 1;0} \right)\).
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \frac{{\left| {2.1 + \left( { - 1} \right).\left( { - 1} \right) + \left( { - 2} \right).0} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} }} = \frac{3}{{3\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\).
Suy ra ((P), (Q)) = 45°.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
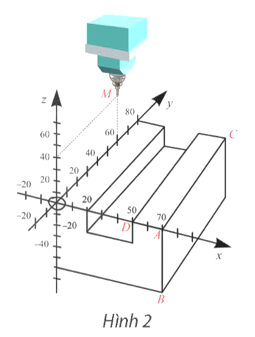
a) Ta có A(70; 0; 0), B(70; 0; −60), C(70; 80; 0), D(50; 0; 0).
b) Ta có \(\overrightarrow {AB} = \left( {0;0; - 60} \right),\overrightarrow {AC} = \left( {0;80;0} \right)\), \(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {4800;0;0} \right)\).
Mặt phẳng (ABC) đi qua A(70; 0; 0), nhận \(\overrightarrow n = \frac{1}{{4800}}\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {1;0;0} \right)\) có phương trình là x – 70 = 0.
Có \(\overrightarrow {AC} = \left( {0;80;0} \right)\), \(\overrightarrow {AD} = \left( { - 20;0;0} \right)\), \(\left[ {\overrightarrow {AC} ,\overrightarrow {AD} } \right] = \left( {0;0;1600} \right)\).
Mặt phẳng (ACD) đi qua A(70; 0; 0), nhận \(\overrightarrow n = \frac{1}{{1600}}\left[ {\overrightarrow {AC} ,\overrightarrow {AD} } \right] = \left( {0;0;1} \right)\) có phương trình là z = 0.
c) Đường thẳng AC đi qua A(70; 0; 0) và nhận \(\overrightarrow a = \frac{1}{{80}}\overrightarrow {AC} = \left( {0;1;0} \right)\) có phương trình tham số là \(\left\{ \begin{array}{l}x = 70\\y = t\\z = 0\end{array} \right.\).
d) \(d\left( {M,\left( {ABC} \right)} \right) = \frac{{\left| {0 - 70} \right|}}{{\sqrt {{1^2}} }} = 70\).
Lời giải
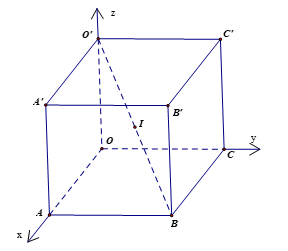
a) Mặt phẳng đoạn chắn của (O'AC) là \(\frac{x}{2} + \frac{y}{6} + \frac{z}{4} = 1\) Û 6x + 2y + 3z – 12 = 0.
b) Đường thẳng CO' đi qua C(0; 6; 0) nhận \(\frac{1}{2}\overrightarrow {CO'} = \left( {0; - 3;2} \right)\) làm vectơ chỉ phương có phương trình là \(\left\{ \begin{array}{l}x = 0\\y = 6 - 3t\\z = 2t\end{array} \right.\).
c) Mặt cầu đi qua các đỉnh của hình hộp có tâm I là trung điểm của O'B và bán kính IO'.
Có B(2; 6; 0), O'(0; 0; 4). Suy ra I(1; 3; 2) và \(IO' = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 3} \right)}^2} + {{\left( {4 - 2} \right)}^2}} = \sqrt {14} \).
Phương trình mặt cầu là: (x – 1)2 + (y – 3)2 + (z – 2)2 = 14.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.