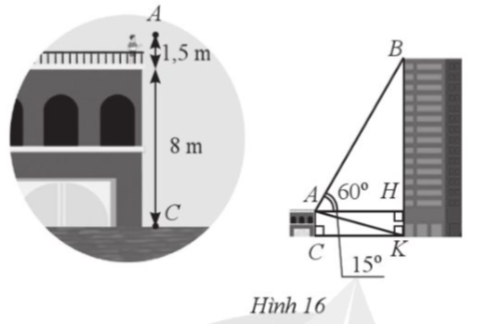
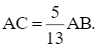Cho tam giác ABC có AB = 6 cm,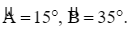 
Tính độ dài đường cao CH của tam giác ABC (làm tròn kết quả đến hàng phần trăm của centimét).
Cho tam giác ABC có AB = 6 cm, Tính độ dài đường cao CH của tam giác ABC (làm tròn kết quả đến hàng phần trăm của centimét).
Quảng cáo
Trả lời:
Giải bởi Vietjack
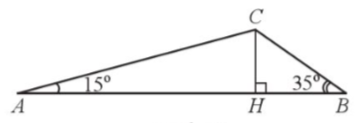
Do CH là đường cao tam giác ABC nên CH ⊥ AB tại H.
Tam giác ACH vuông tại H nên 
Tam giác BCH vuông tại H nên 
Mà AH + BH = AB
Suy ra CH.cot15° + CH.cot35° = AB hay CH(cot15° + cot35°) = AB
Suy ra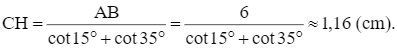 
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
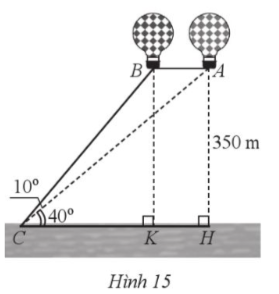
Vì tam giác ACH vuông tại H nên 
Ta có: 
Vì tam giác BCK vuông tại K nên 
Do BK ⊥ CH tại K, AH ⊥ CH tại H suy ra BK // AH.
Mà BK = AH = 350 m
Nên ABKH là hình bình hành.
Suy ra khoảng cách giữa hai khinh khí cầu là:
AB = HK = CH ‒ CK
= 350.cot 40° ‒ 350.cot 50°
= 350.(cot 40° ‒ cot 50°)
≈ 123 m.
Vậy khoảng cách giữa hai khinh khí cầu là khoảng 123 mét.
Lời giải
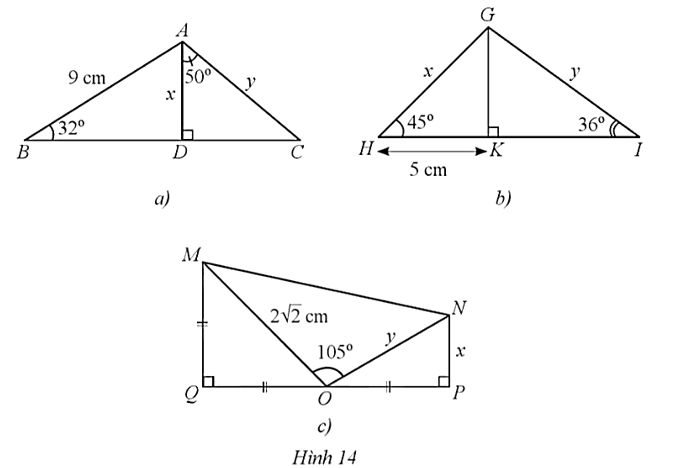
⦁ Hình 14a):
Trong tam giác ABD vuông tại D có:
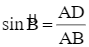hay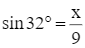 
Suy ra x = 9.sin 32° ≈ 4,8 cm.
Trong tam giác ADC vuông tại D có:
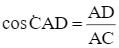hay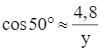 
Suy ra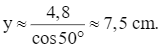 
⦁ Hình 14b):
Trong tam giác GHK vuông tại K có 
nên tam giác GHK vuông cân tại K.
Suy ra GK = HK = 5 cm.
Áp dụng định lí Pythagore cho tam giác GHK vuông tại K, ta có:
HG2 = HK2 + GK2 = 52 + 52 = 50.
Suy ra 
hay x ≈ 7,1 cm.
Trong tam giác GIK vuông tại K có:
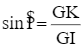hay 
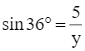
Suy ra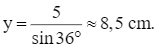 
⦁ Hình 14c):
Trong tam giác MOQ vuông cân tại Q có:
MO2 = QM2 + QO2 hay 
Do đó 2QM2 = 8 nên QM2 = 4
Suy ra OP = QO = QM = 2 cm.
Mặt khác, 
Mà 
(do tam giác MOQ vuông cân tại Q) và 
Suy ra 
Trong tam giác ONP vuông tại P có:
⦁ 
⦁ 
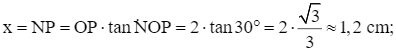
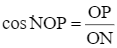suy ra
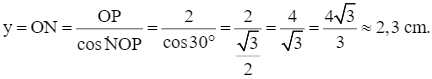
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo