Câu hỏi:
13/07/2024 1,358
Bạn Đức đứng trên nóc ngôi nhà ở độ cao 8 m. Vị trí mắt bạn Đức (tại vị trí A) cách nóc nhà 1,5 m. Bạn nhìn thấy vị trí B cao nhất của một toà nhà với góc tạo bởi tia AB và tia AH theo phương nằm ngang là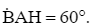 
Bạn Đức cũng nhìn thấy vi trí K tại chân toà nhà đó với góc tạo bới tia AK và tia AH là 
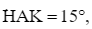AH vuông góc với BK tại H (Hình 10). Tính chiều cao BK của toà nhà (làm tròn kết quả đến hàng phần mười của mét).
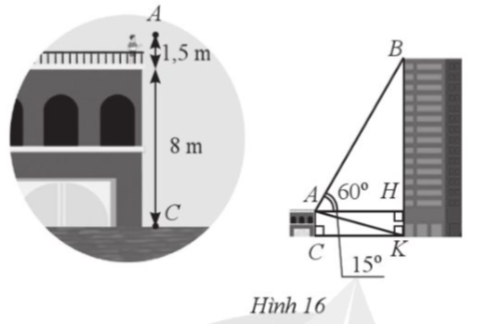
Bạn Đức đứng trên nóc ngôi nhà ở độ cao 8 m. Vị trí mắt bạn Đức (tại vị trí A) cách nóc nhà 1,5 m. Bạn nhìn thấy vị trí B cao nhất của một toà nhà với góc tạo bởi tia AB và tia AH theo phương nằm ngang là Bạn Đức cũng nhìn thấy vi trí K tại chân toà nhà đó với góc tạo bới tia AK và tia AH là AH vuông góc với BK tại H (Hình 10). Tính chiều cao BK của toà nhà (làm tròn kết quả đến hàng phần mười của mét).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Do AH ⊥ BK tại H, AC ⊥ CK, CK ⊥ BK nên 
Do đó tứ giác ACHK là hình chữ nhật.
Suy ra HK = AC = 1,5 + 8 = 9,5 m.
Vì ∆AHK vuông tại H nên 
Vì ∆AHB vuông tại H nên 
Chiều cao của toà nhà là:
BK = HK + BH
= 9,5 + 9,5.cot 15°.tan 60°
= 9,5.(1 + cot 15°.tan 60°)
≈ 70,9 (m).
Vậy chiều cao của tòa nhà khoảng 70,9 mét.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vì tam giác ACH vuông tại H nên 
Ta có: 
Vì tam giác BCK vuông tại K nên 
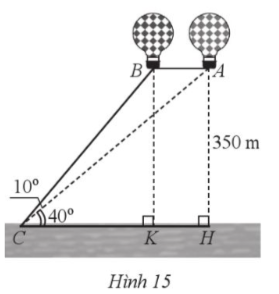
Do BK ⊥ CH tại K, AH ⊥ CH tại H suy ra BK // AH.
Mà BK = AH = 350 m
Nên ABKH là hình bình hành.
Suy ra khoảng cách giữa hai khinh khí cầu là:
AB = HK = CH ‒ CK
= 350.cot 40° ‒ 350.cot 50°
= 350.(cot 40° ‒ cot 50°)
≈ 123 m.
Vậy khoảng cách giữa hai khinh khí cầu là khoảng 123 mét.
Lời giải
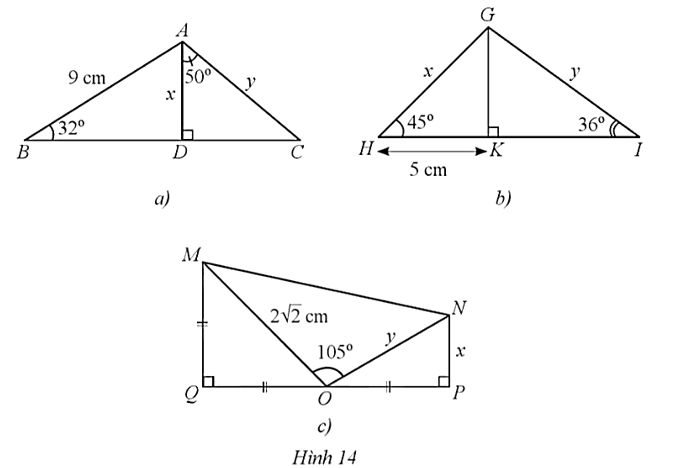
⦁ Hình 14a):
Trong tam giác ABD vuông tại D có:
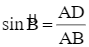hay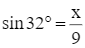 
Suy ra x = 9.sin 32° ≈ 4,8 cm.
Trong tam giác ADC vuông tại D có:
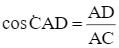hay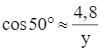 
Suy ra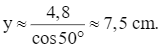 
⦁ Hình 14b):
Trong tam giác GHK vuông tại K có 
nên tam giác GHK vuông cân tại K.
Suy ra GK = HK = 5 cm.
Áp dụng định lí Pythagore cho tam giác GHK vuông tại K, ta có:
HG2 = HK2 + GK2 = 52 + 52 = 50.
Suy ra 
hay x ≈ 7,1 cm.
Trong tam giác GIK vuông tại K có:
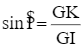hay 
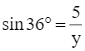
Suy ra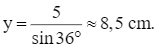 
⦁ Hình 14c):
Trong tam giác MOQ vuông cân tại Q có:
MO2 = QM2 + QO2 hay 
Do đó 2QM2 = 8 nên QM2 = 4
Suy ra OP = QO = QM = 2 cm.
Mặt khác, 
Mà 
(do tam giác MOQ vuông cân tại Q) và 
Suy ra 
Trong tam giác ONP vuông tại P có:
⦁ 
⦁ 
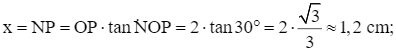
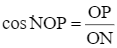suy ra
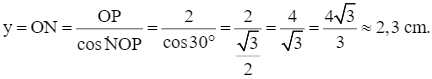
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận