Gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II. Tính xác suất của các biến cố sau:
G: “Không có con xúc xắc nào xuất hiện mặt 6 chấm”;
H: “Số chấm xuất hiện con xúc xắc I là số lẻ và số chấm xuất hiện trên con xúc xắc II lớn hơn 4”;
K: “Số chấm xuất hiện trên cả hai con xúc xắc lớn hơn 2”.
Gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II. Tính xác suất của các biến cố sau:
G: “Không có con xúc xắc nào xuất hiện mặt 6 chấm”;
H: “Số chấm xuất hiện con xúc xắc I là số lẻ và số chấm xuất hiện trên con xúc xắc II lớn hơn 4”;
K: “Số chấm xuất hiện trên cả hai con xúc xắc lớn hơn 2”.
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Luyện tập chung trang 64 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Không gian mẫu \(\Omega \) = {(a, b), 1 ≤ a, b ≤ 6 trong đó a và b là các số tự nhiên}.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
|
Xúc xắc II Xúc xắc I |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
(1, 1) |
(1, 2) |
(1, 3) |
(1, 4) |
(1, 5) |
(1, 6) |
|
2 |
(2, 1) |
(2, 2) |
(2, 3) |
(2, 4) |
(2, 5) |
(2, 6) |
|
3 |
(3, 1) |
(3, 2) |
(3, 3) |
(3, 4) |
(3, 5) |
(3, 6) |
|
4 |
(4, 1) |
(4, 2) |
(4, 3) |
(4, 4) |
(4, 5) |
(4, 6) |
|
5 |
(5, 1) |
(5, 2) |
(5, 3) |
(5, 4) |
(5, 5) |
(5, 6) |
|
6 |
(6, 1) |
(6, 2) |
(6, 3) |
(6, 4) |
(6, 5) |
(6, 6) |
Mỗi ô trong bảng là một kết quả có thể. Có 36 kết quả có thể là đồng khả năng.
− Các kết quả thuận lợi cho biến cố G là các cặp số (a, b), trong đó 1 ≤ a, b ≤ 5.
Có 25 kết quả thuận lợi cho biến cố G. Vậy \(P\left( G \right) = \frac{{25}}{{36}}.\)
− Có 6 kết quả thuận lợi cho biến cố H là (1, 5); (3, 5); (5, 5); (1, 6); (3, 6); (5, 6).
Vậy \(P\left( H \right) = \frac{6}{{36}} = \frac{1}{6}.\)
− Các kết quả thuận lợi cho biến cố K là các cặp số (a, b) trong đó 3 ≤ a, b ≤ 6.
Có 32 kết quả thuận lợi cho biến cố K. Vậy \(P\left( K \right) = \frac{{32}}{{36}} = \frac{8}{9}.\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
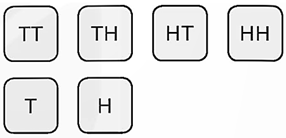
Ta lập bảng sau:
|
Túi I Túi II |
TT |
TH |
HT |
HH |
|
T |
TTT |
TTH |
THT |
THH |
|
H |
HTT |
HTH |
HHT |
HHH |
Mỗi ô trong bảng là một kết quả có thể.
Không gian mẫu \(\Omega \) = {TTT; TTH; THT; THH; HTT; HTH; HHT; HHH}.
Có 8 kết quả có thể là đồng khả năng.
a) Có 3 kết quả thuận lợi cho biến cố E là THH; HTH; HHT. Vậy \(P\left( E \right) = \frac{3}{8}.\)
b) Có 7 kết quả thuận lợi cho biến cố F là HHH; HHT; HTH; HTT; THH; THT; TTH. Vậy \(P\left( F \right) = \frac{7}{8}.\)
Lời giải
Kí hiệu ba nam là A, B, C và hai nữ là D, E. Mỗi kết quả có thể là cặp (X, Y) trong đó X, Y tương ứng là tên của ứng viên được chọn lần đầu và lần thứ hai với X ≠ Y.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng sau:
|
Lần 2 Lần 1 |
A |
B |
C |
D |
E |
|
A |
|
(A, B) |
(A, C) |
(A, D) |
(A, E) |
|
B |
(B, A) |
|
(B, C) |
(B, D) |
(B, E) |
|
C |
(C, A) |
(C, B) |
|
(C, D) |
(C, E) |
|
D |
(D, A) |
(D, B) |
(D, C) |
|
(D, E) |
|
E |
(E, A) |
(E, B) |
(E, C) |
(E, D) |
|
Vì X ≠ Y nên cặp có hai phần tử trùng nhau không được tính, tức là trong bảng ta phải xóa 5 ô (A, A); (B, B); (C, C); (D, D); (E, E).
Vậy có 20 kết quả có thể là đồng khả năng.
Có 12 kết quả thuận lợi cho biến cố “chọn được một nam, một nữ” là (A, D); (A, E); (B, D); (B, E); (C, D); (C, E); (D, A); (D, B); (D, C); (E, A); (E, B); (E, C).
Vậy xác suất cần tìm là \(\frac{{12}}{{20}} = \frac{3}{5}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo