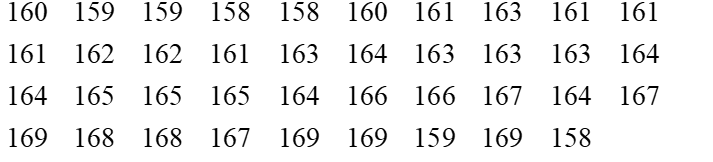Tìm hiểu thời gian (đơn vị: giờ) truy cập Internet trong tuần đầu tháng 4 của một số cán bộ ở một viện nghiên cứu thu được kết quả như ở Bảng 32 sau:
Thời gian
[0; 5)
[5; 10)
[10; 15)
[15; 20)
[20; 25)
Số người
5
20
15
6
4
Bảng 32
a) Lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó.
b) Vẽ biểu đồ tần số ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm đó.
c) Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó.
Tìm hiểu thời gian (đơn vị: giờ) truy cập Internet trong tuần đầu tháng 4 của một số cán bộ ở một viện nghiên cứu thu được kết quả như ở Bảng 32 sau:
|
Thời gian |
[0; 5) |
[5; 10) |
[10; 15) |
[15; 20) |
[20; 25) |
|
Số người |
5 |
20 |
15 |
6 |
4 |
Bảng 32
a) Lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó.
b) Vẽ biểu đồ tần số ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm đó.
c) Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó.
Quảng cáo
Trả lời:
a) Mẫu dữ liệu thống kê đó có 50 dữ liệu (N = 50) và có năm nửa khoảng [0; 5), [5; 10), [10; 15), [15; 20), [20; 25).
Các giá trị năm nửa khoảng [0; 5), [5; 10), [10; 15), [15; 20), [20; 25) lần lượt có tần số là:
n1 = 5; n2 = 20; n3 = 15; n4 = 6; n5 = 4.
Bảng tần số ghép nhóm của mẫu số liệu đó sau khi ghép nhóm theo năm nhóm ứng với năm nửa khoảng [0; 5), [5; 10), [10; 15), [15; 20), [20; 25) như sau:
|
Nhóm |
[0; 5) |
[5; 10) |
[10; 15) |
[15; 20) |
[20; 25) |
Cộng |
|
Tần số (n) |
5 |
20 |
15 |
6 |
4 |
N = 50 |
Các giá trị năm nửa khoảng [0; 5), [5; 10), [10; 15), [15; 20), [20; 25) lần lượt có tần số tương đối là:
\[{f_1} = \frac{{5 \cdot 100}}{{50}}\% = 10\% ;\] \[{f_2} = \frac{{20 \cdot 100}}{{50}}\% = 40\% ;\] \[{f_3} = \frac{{15 \cdot 100}}{{50}}\% = 30\% ;\] \[{f_4} = \frac{{6 \cdot 100}}{{50}}\% = 12\% ;\] \[{f_5} = \frac{{4 \cdot 100}}{{50}}\% = 8\% .\]
Bảng tần số tương đối ghép nhóm:
|
Nhóm |
[0; 5) |
[5; 10) |
[10; 15) |
[15; 20) |
[20; 25) |
Cộng |
|
Tần số tương đối (%) |
10 |
40 |
30 |
12 |
8 |
100 |
b) Biểu đồ tần số ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm đó như sau:
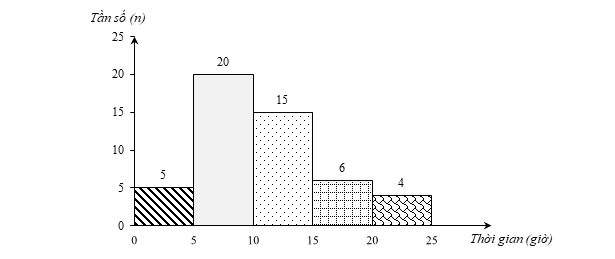
c) Biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó như sau:
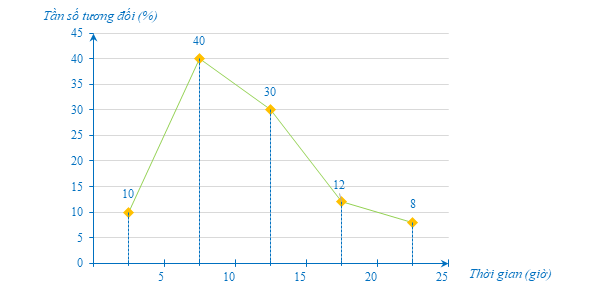
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
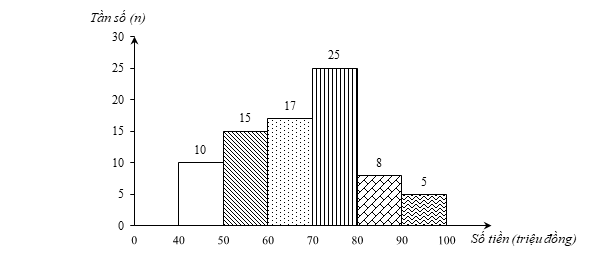
a) Mẫu dữ liệu thống kê đó có 80 dữ liệu (N = 80) và có sáu nửa khoảng [40; 50), [50; 60), [60; 70), [70; 80), [80; 90), [90; 100).
Các giá trị năm nửa khoảng [40; 50), [50; 60), [60; 70), [70; 80), [80; 90), [90; 100) lần lượt có tần số là:
n1 = 10; n2 = 15; n3 = 17; n4 = 25; n5 = 8; n6 = 5.
Các giá trị năm nửa khoảng [40; 50), [50; 60), [60; 70), [70; 80), [80; 90), [90; 100) lần lượt có tần số tương đối là:
\[{f_1} = \frac{{10 \cdot 100}}{{80}}\% = 12,5\% ;\] \[{f_2} = \frac{{15 \cdot 100}}{{80}}\% = 18,75\% ;\] \[{f_3} = \frac{{17 \cdot 100}}{{80}}\% = 21,25\% ;\] \[{f_4} = \frac{{25 \cdot 100}}{{80}}\% = 31,25\% ;\] \[{f_5} = \frac{{8 \cdot 100}}{{80}}\% = 10\% ;\] \[{f_6} = \frac{{5 \cdot 100}}{{80}}\% = 6,25\% .\]
Bảng tần số ghép nhóm tương đối của mẫu số liệu đó sau khi ghép nhóm theo sáu nhóm ứng với sáu nửa khoảng [40; 50), [50; 60), [60; 70), [70; 80), [80; 90), [90; 100) như sau:
|
Nhóm |
[40; 50) |
[50; 60) |
[60; 70) |
[70; 80) |
[80; 90) |
[90; 100) |
Cộng |
|
Tần số tương đối (%) |
12,5 |
18,75 |
21,25 |
31,25 |
10 |
6,25 |
100 |
b) Biểu đồ tương đối ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm đó như sau:
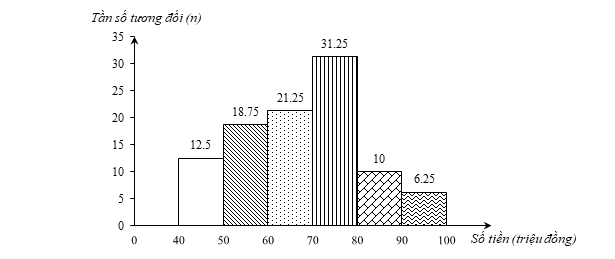
Lời giải
a) Ta có thể ghép nhóm mẫu số liệu đã cho theo năm nhóm ứng với năm nửa khoảng [6,0; 6,5), [6,5; 7,0), [7,0; 7,5), [7,5; 8,0), [8,0; 8,5) như sau:
|
Nhóm |
[6,0; 6,5) |
[6,5; 7,0) |
[7,0; 7,5) |
[7,5; 8,0) |
[8,0; 8,5) |
|
Số liệu |
6,3; 6,2; 6,0; 6,1 |
6,5; 6,6; 6,7; 6,8; 6,9; 6,7; 6,9; 6,9; 6,6; 6,8 |
7,2; 7,3; 7,3; 7,0; 7,4; 7,0; 7,4; 7,2; 7,1; 7,1; 7,4; 7,2 |
7,7; 7,6; 7,8; 7,8; 7,9; 7,9; 7,8; 7,5 |
8,0; 8,3; 8,2; 8,2; 8,4; 8,1 |
b) Mẫu dữ liệu thống kê đó có 40 dữ liệu (N = 40) và có năm nửa khoảng [6,0; 6,5), [6,5; 7,0), [7,0; 7,5), [7,5; 8,0), [8,0; 8,5).
Các giá trị năm nửa khoảng [6,0; 6,5), [6,5; 7,0), [7,0; 7,5), [7,5; 8,0), [8,0; 8,5) lần lượt có tần số là:
n1 = 4; n2 = 10; n3 = 12; n4 = 8; n5 = 6.
Bảng tần số ghép nhóm của mẫu số liệu ghép nhóm đó như sau:
|
Nhóm |
[6,0; 6,5) |
[6,5; 7,0) |
[7,0; 7,5) |
[7,5; 8,0) |
[8,0; 8,5) |
Cộng |
|
Tần số (n) |
4 |
10 |
12 |
8 |
6 |
N = 40 |
Các giá trị năm nửa khoảng [6,0; 6,5), [6,5; 7,0), [7,0; 7,5), [7,5; 8,0), [8,0; 8,5) lần lượt có tần số tương đối là:
\[{f_1} = \frac{{4 \cdot 100}}{{40}}\% = 10\% ;\] \[{f_2} = \frac{{10 \cdot 100}}{{40}}\% = 25\% ;\] \[{f_3} = \frac{{12 \cdot 100}}{{40}}\% = 30\% ;\] \[{f_4} = \frac{{8 \cdot 100}}{{40}}\% = 20\% ;\] \[{f_5} = \frac{{6 \cdot 100}}{{40}}\% = 15\% .\]
Bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó như sau:
|
Nhóm |
[6,0; 6,5) |
[6,5; 7,0) |
[7,0; 7,5) |
[7,5; 8,0) |
[8,0; 8,5) |
Cộng |
|
Tần số tương đối (%) |
10 |
25 |
30 |
20 |
15 |
100 |
c) Biểu đồ tần số ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm nêu ở câu a như sau:
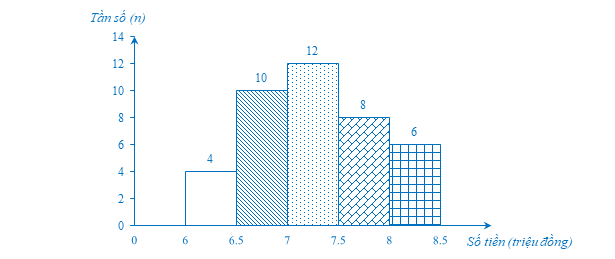
d) Biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm nêu ở câu a như sau:
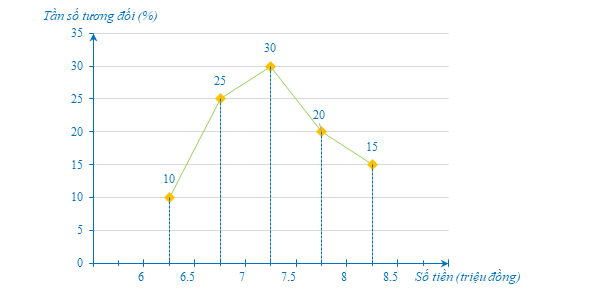
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.