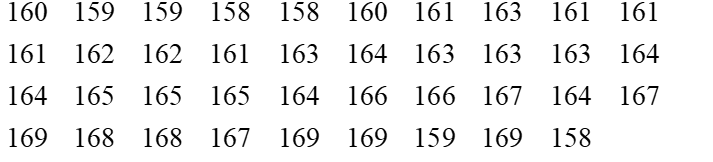Giải SBT Toán 9 Cánh diều Bài 3. Tần số ghép nhóm. Tần số tương đối ghép nhóm có đáp án
31 người thi tuần này 4.6 326 lượt thi 5 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: B
Trong mẫu số liệu đó, số liệu có giá trị nhỏ nhất là 158, số liệu có giá trị lớn nhất là 170. Vì thế, ta chọn nửa khoảng [158; 170) sao cho giá trị của mỗi số liệu trong mẫu số liệu đều thuộc nửa khoảng [158; 170). Vì độ dài của nửa khoảng [158; 170) bằng 170 – 158 = 12 nên ta có thể phân chia nửa khoảng đó thành sáu nửa khoảng có độ dài bằng nhau là: [158; 160), [160; 162), [162; 164), [164; 166), [166; 168), [168; 170).
Lời giải
Đáp án đúng là: C
Mẫu số liệu được chia thành 6 nhóm là: [5; 10), [10; 15), [15; 20), [20; 25), [25; 30), [30; 35).
Lời giải
a) Ta có thể ghép nhóm mẫu số liệu đã cho theo năm nhóm ứng với năm nửa khoảng [6,0; 6,5), [6,5; 7,0), [7,0; 7,5), [7,5; 8,0), [8,0; 8,5) như sau:
|
Nhóm |
[6,0; 6,5) |
[6,5; 7,0) |
[7,0; 7,5) |
[7,5; 8,0) |
[8,0; 8,5) |
|
Số liệu |
6,3; 6,2; 6,0; 6,1 |
6,5; 6,6; 6,7; 6,8; 6,9; 6,7; 6,9; 6,9; 6,6; 6,8 |
7,2; 7,3; 7,3; 7,0; 7,4; 7,0; 7,4; 7,2; 7,1; 7,1; 7,4; 7,2 |
7,7; 7,6; 7,8; 7,8; 7,9; 7,9; 7,8; 7,5 |
8,0; 8,3; 8,2; 8,2; 8,4; 8,1 |
b) Mẫu dữ liệu thống kê đó có 40 dữ liệu (N = 40) và có năm nửa khoảng [6,0; 6,5), [6,5; 7,0), [7,0; 7,5), [7,5; 8,0), [8,0; 8,5).
Các giá trị năm nửa khoảng [6,0; 6,5), [6,5; 7,0), [7,0; 7,5), [7,5; 8,0), [8,0; 8,5) lần lượt có tần số là:
n1 = 4; n2 = 10; n3 = 12; n4 = 8; n5 = 6.
Bảng tần số ghép nhóm của mẫu số liệu ghép nhóm đó như sau:
|
Nhóm |
[6,0; 6,5) |
[6,5; 7,0) |
[7,0; 7,5) |
[7,5; 8,0) |
[8,0; 8,5) |
Cộng |
|
Tần số (n) |
4 |
10 |
12 |
8 |
6 |
N = 40 |
Các giá trị năm nửa khoảng [6,0; 6,5), [6,5; 7,0), [7,0; 7,5), [7,5; 8,0), [8,0; 8,5) lần lượt có tần số tương đối là:
\[{f_1} = \frac{{4 \cdot 100}}{{40}}\% = 10\% ;\] \[{f_2} = \frac{{10 \cdot 100}}{{40}}\% = 25\% ;\] \[{f_3} = \frac{{12 \cdot 100}}{{40}}\% = 30\% ;\] \[{f_4} = \frac{{8 \cdot 100}}{{40}}\% = 20\% ;\] \[{f_5} = \frac{{6 \cdot 100}}{{40}}\% = 15\% .\]
Bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó như sau:
|
Nhóm |
[6,0; 6,5) |
[6,5; 7,0) |
[7,0; 7,5) |
[7,5; 8,0) |
[8,0; 8,5) |
Cộng |
|
Tần số tương đối (%) |
10 |
25 |
30 |
20 |
15 |
100 |
c) Biểu đồ tần số ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm nêu ở câu a như sau:
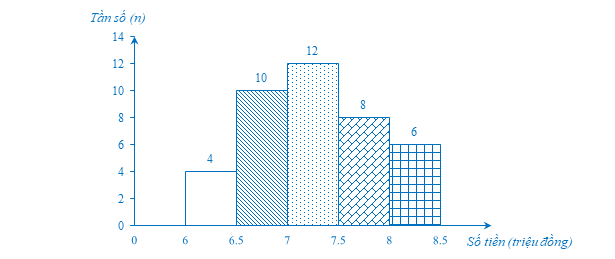
d) Biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm nêu ở câu a như sau:
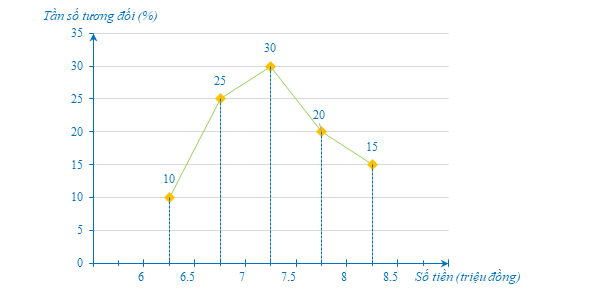
Lời giải
a) Mẫu dữ liệu thống kê đó có 50 dữ liệu (N = 50) và có năm nửa khoảng [0; 5), [5; 10), [10; 15), [15; 20), [20; 25).
Các giá trị năm nửa khoảng [0; 5), [5; 10), [10; 15), [15; 20), [20; 25) lần lượt có tần số là:
n1 = 5; n2 = 20; n3 = 15; n4 = 6; n5 = 4.
Bảng tần số ghép nhóm của mẫu số liệu đó sau khi ghép nhóm theo năm nhóm ứng với năm nửa khoảng [0; 5), [5; 10), [10; 15), [15; 20), [20; 25) như sau:
|
Nhóm |
[0; 5) |
[5; 10) |
[10; 15) |
[15; 20) |
[20; 25) |
Cộng |
|
Tần số (n) |
5 |
20 |
15 |
6 |
4 |
N = 50 |
Các giá trị năm nửa khoảng [0; 5), [5; 10), [10; 15), [15; 20), [20; 25) lần lượt có tần số tương đối là:
\[{f_1} = \frac{{5 \cdot 100}}{{50}}\% = 10\% ;\] \[{f_2} = \frac{{20 \cdot 100}}{{50}}\% = 40\% ;\] \[{f_3} = \frac{{15 \cdot 100}}{{50}}\% = 30\% ;\] \[{f_4} = \frac{{6 \cdot 100}}{{50}}\% = 12\% ;\] \[{f_5} = \frac{{4 \cdot 100}}{{50}}\% = 8\% .\]
Bảng tần số tương đối ghép nhóm:
|
Nhóm |
[0; 5) |
[5; 10) |
[10; 15) |
[15; 20) |
[20; 25) |
Cộng |
|
Tần số tương đối (%) |
10 |
40 |
30 |
12 |
8 |
100 |
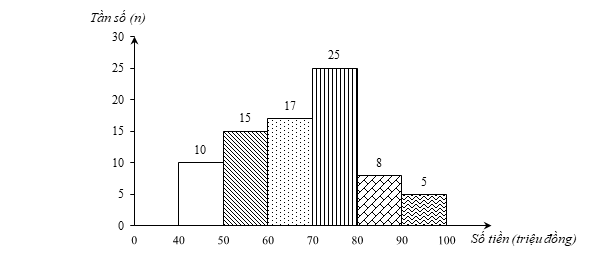
b) Biểu đồ tần số ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm đó như sau:
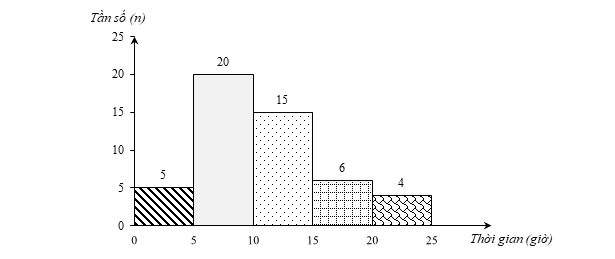
c) Biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó như sau:
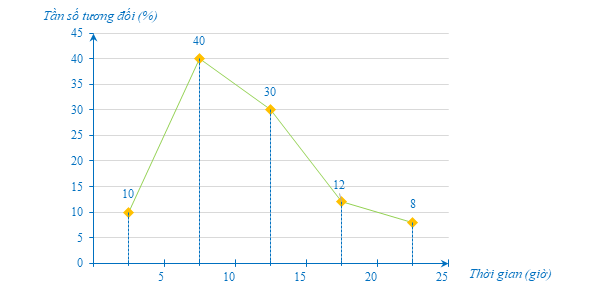
Lời giải
a) Mẫu dữ liệu thống kê đó có 80 dữ liệu (N = 80) và có sáu nửa khoảng [40; 50), [50; 60), [60; 70), [70; 80), [80; 90), [90; 100).
Các giá trị năm nửa khoảng [40; 50), [50; 60), [60; 70), [70; 80), [80; 90), [90; 100) lần lượt có tần số là:
n1 = 10; n2 = 15; n3 = 17; n4 = 25; n5 = 8; n6 = 5.
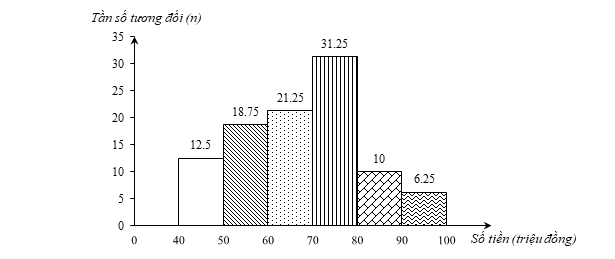
Các giá trị năm nửa khoảng [40; 50), [50; 60), [60; 70), [70; 80), [80; 90), [90; 100) lần lượt có tần số tương đối là:
\[{f_1} = \frac{{10 \cdot 100}}{{80}}\% = 12,5\% ;\] \[{f_2} = \frac{{15 \cdot 100}}{{80}}\% = 18,75\% ;\] \[{f_3} = \frac{{17 \cdot 100}}{{80}}\% = 21,25\% ;\] \[{f_4} = \frac{{25 \cdot 100}}{{80}}\% = 31,25\% ;\] \[{f_5} = \frac{{8 \cdot 100}}{{80}}\% = 10\% ;\] \[{f_6} = \frac{{5 \cdot 100}}{{80}}\% = 6,25\% .\]
Bảng tần số ghép nhóm tương đối của mẫu số liệu đó sau khi ghép nhóm theo sáu nhóm ứng với sáu nửa khoảng [40; 50), [50; 60), [60; 70), [70; 80), [80; 90), [90; 100) như sau:
|
Nhóm |
[40; 50) |
[50; 60) |
[60; 70) |
[70; 80) |
[80; 90) |
[90; 100) |
Cộng |
|
Tần số tương đối (%) |
12,5 |
18,75 |
21,25 |
31,25 |
10 |
6,25 |
100 |
b) Biểu đồ tương đối ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm đó như sau: