Cho tam giác ABC có AB = AC = 13 cm, BC = 10 cm và có BH, CK là hai đường cao. Chứng minh:
a) Bốn điểm B, C, H, K cùng nằm trên đường tròn (O; R).
b) Điểm A nằm ngoài đường tròn (O; R).
Cho tam giác ABC có AB = AC = 13 cm, BC = 10 cm và có BH, CK là hai đường cao. Chứng minh:
a) Bốn điểm B, C, H, K cùng nằm trên đường tròn (O; R).
b) Điểm A nằm ngoài đường tròn (O; R).
Quảng cáo
Trả lời:
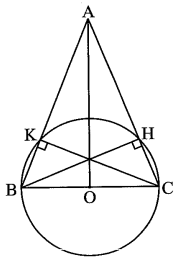
a) Gọi O là trung điểm của BC. Khi đó, \(OB = OC = \frac{1}{2}BC.\)
Do BH và CK là đường cao tam giác ABC nên BH ⊥ AC tại H; CK ⊥ AB tại K
Suy ra tam giác BHC vuông tại H; tam giác BKC vuông tại K
Xét tam giác BKC vuông tại H có KO là đường trung tuyến ứng với cạnh huyền BC nên \(KO = \frac{1}{2}BC.\)
Chứng minh tương tự đối với ∆BKC vuông tại K, ta có \(HO = \frac{1}{2}BC.\)
Suy ra \[KO = OH = OB = OC = \frac{1}{2}BC = \frac{1}{2} \cdot 10 = 5\,\,{\rm{(cm}}).\]
Tứ giác BKHC có: OB = OK = OH = OC = 5 cm nên bốn điểm B, C, H, K cùng nằm trên đường tròn (O; R) với R = 5 cm.
b) Xét ∆ABC cân tại A (do AB = AC) có AO là đường trung tuyến nên đồng thời là đường cao, suy ra ∆ABO vuông tại O.
Áp dụng định lí Pythagore cho tam giác AOB vuông tại O, ta có:
\(OA = \sqrt {B{A^2} - O{B^2}} = \sqrt {{{13}^2} - {5^2}} = \sqrt {144} = 12\,\,({\rm{cm}}).\)
Vì 12 > 5 nên OA > R, suy ra điểm A nằm ngoài đường tròn (O; R).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
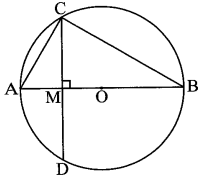
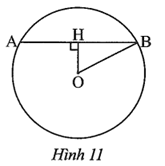
a) Ta có đường kính AB là trục đối xứng của đường tròn (O)
Suy ra \(MC = MD = \frac{{CD}}{2} = \frac{{2\sqrt 3 }}{2} = \sqrt 3 \;({\rm{cm}}).\)
Tam giác ABC có CO là đường trung tuyến và \(CO = \frac{1}{2}AB,\) suy ra ABC là tam giác vuông tại C.
Do \[\widehat {CAM} + \widehat {CBM} = 90^\circ ;\,\,\widehat {CAM} + \widehat {ACM} = 90^\circ \] nên \[\widehat {CBM} = \widehat {ACM}.\]
Xét ∆CMB và ∆AMC có:
\[\widehat {AMC} = \widehat {CMB} = 90^\circ \] và \[\widehat {CBM} = \widehat {ACM}\]
Do đó ∆CMB ᔕ ∆AMC (g.g).
Suy ra \(\frac{{MC}}{{MA}} = \frac{{MB}}{{MC}},\) nên \(MB = \frac{{M{C^2}}}{{MA}} = \frac{{{{\left( {\sqrt 3 } \right)}^2}}}{1} = 3\;({\rm{cm}}).\)
Gọi R là bán kính đường tròn đường kính AB, khi đó AB = 2R.
Ta có AB = MA + MB = 1 + 3 = 4 = 2R, suy ra R = 2 cm.
b) Xét tam giác AMC vuông tại M, ta có:
\(\tan \widehat {CAB} = \tan \widehat {CAM} = \frac{{MC}}{{MA}} = \frac{{\sqrt 3 }}{1} = \sqrt 3 ,\) suy ra \(\widehat {CAB} \approx 60^\circ .\)
Lời giải
a) Ta có: 7 < 29 – 4 nên OO’ < R – R’, suy ra đường tròn (O; R) đựng đường tròn (O’; R’).
b) Ta có: 21 = 44 – 23 nên OO’ = R – R’, suy ra hai đường tròn (O; R) và (O’; R’) tiếp xúc trong.
c) Ta có: 15 = 7 + 8 nên OO’ = R + R’, suy ra hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài.
d) Ta có: 24 – 20 < 6 < 24 + 20 nên R – R’ < OO’ < R + R’, suy ra hai đường tròn (O; R) và (O’; R’) cắt nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.