Cho đường tròn (O; R) và dây cung \(MN = R\sqrt 3 .\) Tính số đo của mỗi cung (cung lớn và cung nhỏ).
Cho đường tròn (O; R) và dây cung \(MN = R\sqrt 3 .\) Tính số đo của mỗi cung (cung lớn và cung nhỏ).
Quảng cáo
Trả lời:
Giải bởi Vietjack
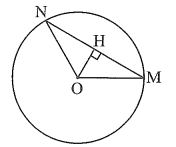
Kẻ OH ⊥ MN tại H.
Xét ∆OMN cân tại O (do OM = ON = R) có OH là đường cao nên đồng thời là đường trung tuyến, hay H là trung điểm của MN.
Do đó \(HM = HN = \frac{{MN}}{2} = \frac{{R\sqrt 3 }}{2}.\)
Xét ∆HMO vuông tại H, có:
\(\cos \widehat {HMO} = \frac{{HM}}{{OM}} = \frac{{\frac{{R\sqrt 3 }}{2}}}{R} = \frac{{\sqrt 3 }}{2},\) nên \(\widehat {HMO} = 30^\circ \)
Mà ∆OMN cân tại O nên ta có:
\(\widehat {MON} = 180^\circ - 2\widehat {HMO} = 180^\circ - 2 \cdot 30^\circ = 120^\circ .\)
Suy ra số đo cung nhỏ MN là 120°, số đo cung lớn MN là 360° – 120° = 240°.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
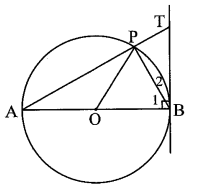
a) Do AB là đường kính của đường tròn (O), P thuộc đường tròn (O), suy ra \(\widehat {APB} = 90^\circ .\)
Do đó \[\widehat {PAB} + \widehat {{B_1}} = 90^\circ \] (1)
Do tia AP cắt tiếp tuyến tại B của đường tròn (O) tại T nên AB ⊥ BT
Do đó \[\widehat {{B_1}} + \widehat {{B_2}} = 90^\circ \] (2)
Từ (1), (2) suy ra \(\widehat {ATB} = \widehat {{B_1}}\)
Mà \(\widehat {{B_1}} = \frac{1}{2}\widehat {AOP}\) (góc nội tiếp và góc ở tâm cùng chắn cung AP) nên \(\widehat {ATB} = \frac{1}{2}\widehat {AOP}\) hay \(\widehat {AOP} = 2\widehat {ATB}.\)
b) Do A, P thuộc đường tròn (O) nên AO = OP, do đó ∆AOP cân tại O, suy ra \(\widehat {PAO} = \widehat {APO}.\)
Mà \(\widehat {PAO} = \widehat {PBT}\) (cùng phụ với \(\widehat {{B_1}}),\) suy ra \(\widehat {APO} = \widehat {\;PBT}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
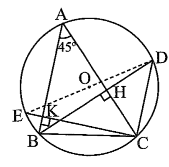
Do BH, CK là đường cao ∆ABC nên BH ⊥ AC, CK ⊥ AB.
Xét ∆ABH vuông tại H có \(\widehat {BAH} = 45^\circ \) nên \(\widehat {ABH} = 90^\circ - \widehat {BAH} = 90^\circ - 45^\circ = 45^\circ .\)
Mặt khác, \(\widehat {ABD} = \widehat {ACD}\) (hai góc nội tiếp cùng chắn cung AD) nên \(\widehat {ACD} = 45^\circ .\) (1)
Tương tự, ta có \(\widehat {ACK} = 90^\circ - \widehat {CAK} = 90^\circ - 45^\circ = 45^\circ .\) (2)
Từ (1) và (2) suy ra \(\widehat {DCE} = \widehat {ACD} + \widehat {ACK} = 45^\circ + 45^\circ = 90^\circ \)
Mà \(\widehat {DCE}\) là góc nội tiếp chắn cung DE nên DE là đường kính của đường tròn (O).
Vậy ba điểm D, O, E thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập