Câu hỏi:

29/08/2024 1,167

1) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{\sqrt {3x + 1} + 2y = 4}\\{3\sqrt {3x + 1} - y = 5.}\end{array}} \right.\)

2) Trong mặt phẳng tọa độ \(Oxy,\) cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = \left( {m - 2} \right)x + 5.\)

a) Chứng minh \[\left( d \right)\] luôn cắt \(\left( P \right)\) tại hai điểm phân biệt.

b) Gọi \({x_1},{x_2}\) là hoành độ các giao điểm của \(\left( d \right)\) và \(\left( P \right).\) Tìm tất cả giá trị của \(m\) để \({x_1} + 5{x_2} = 0.\)

Xem lời giải

Câu hỏi trong đề: Ôn thi Cấp tốc 789+ vào 10 môn Toán khu vực Hà Nội 2024 - 2025 (Đề 11) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

1) \(\left\{ {\begin{array}{*{20}{l}}{\sqrt {3x + 1} + 2y = 4\,\,\,\,\left( 1 \right)}\\{3\sqrt {3x + 1} - y = 5\,\,\,\,\left( 2 \right)}\end{array}} \right.\)

Điều kiện \(x \ge - \frac{1}{3}.\)

Nhân hai vế của phương trình \(\left( 2 \right)\) với \(2,\) ta được hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{\sqrt {3x + 1} + 2y = 4}\\{6\sqrt {3x + 1} - 2y = 10.}\end{array}} \right.\)

Cộng từng vế hai phương trình của hệ phương trình trên, ta được:

\(7\sqrt {3x + 1} = 14,\) suy ra \(\sqrt {3x + 1} = 2\) nên \(3x + 1 = 4,\) do đó \(x = 1\) (thỏa mãn \(x \ge - \frac{1}{3}).\)

Thay \(\sqrt {3x + 1} = 2\) vào phương trình \(\left( 1 \right),\) ta được:

\(2 + 2y = 4,\) do đó \(y = 1.\)

Vậy hệ phương trình có nghiệm duy nhất là \[\left( {1;\,\,1} \right).\]

2) a) Xét phương trình hoành độ giao điểm của \[\left( d \right)\] và \(\left( P \right)\) là:

\({x^2} = \left( {m - 2} \right)x + 5\) hay \({x^2} - \left( {m - 2} \right)x - 5 = 0\)

Phương trình trên có \({\rm{\Delta }} = \left[ { - {{\left( {m - 2} \right)}^2}} \right] - 4 \cdot 1 \cdot \left( { - 5} \right)\)\( = {\left( {m - 2} \right)^2} + 20 > 0\) với mọi \(m \in \mathbb{R}.\)

Do đó phương trình trên luôn có hai nghiệm phân biệt.

Vậy \[\left( d \right)\] luôn cắt \[\left( P \right)\] tại hai điểm phân biệt.

b) Theo định lí Viète, ta có: \[\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = m - 2}\\{{x_1}{x_2} = - 5.}\end{array}} \right.\]

Theo bài, \({x_1} + 5{x_2} = 0\) nên suy ra \({x_1} = - 5{x_2}.\)

Kết hợp với \[{x_1}{x_2} = - 5,\] ta được: \( - 5{x_2} \cdot {x_2} = - 5,\) hay \(x_2^2 = 1,\) nên \({x_2} = 1\) hoặc \({x_2} = - 1.\)

Trường hợp 1. \({x_2} = 1,\) suy ra \({x_1} = - 5,\) kết hợp với \[{x_1} + {x_2} = m - 2,\] ta được:

\( - 5 + 1 = m - 2,\) do đó \(m = - 2.\)

Trường hợp 2. \({x_2} = - 1,\) suy ra \({x_1} = 5,\) kết hợp với \[{x_1} + {x_2} = m - 2,\] ta được:

\(5 + \left( { - 1} \right) = m - 2,\) do đó \(m = 6.\)

Vậy \(m \in \left\{ { - 2;6} \right\}\) là giá trị cần tìm.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

Để chở 15 tấn thiết bị phục vụ Lễ kỷ niệm 70 năm chiến thắng Điện Biên Phủ, một đội vận chuyển dự định sử dụng các xe tải loại nhỏ. Do thay đổi kế hoạch, đội vận chuyển quyết định chỉ sử dụng các xe tải loại lớn. Vì vậy, số xe tải sử dụng giảm đi 2 xe so với dự định và mỗi xe tải loại lớn chở nhiều hơn mỗi xe tải loại nhỏ là 2 tấn. Hỏi đội vận chuyển sử dụng bao nhiêu xe tải loại lớn? (Biết mỗi xe tải cùng loại đều chở số tấn thiết bị bằng nhau).

2) Một bình đựng nước có dạng hình trụ với bán kính đáy là \(4\) cm và chiều cao là \(25{\rm{\;cm}}{\rm{.}}\) Tính diện tích xung quanh của bình đựng nước đó (lấy \(\pi \approx 3,14).\)

Xem đáp án

Lời giải

1) Gọi số xe tải loại lớn mà đội vận chuyển sử dụng là \(x\) (xe) \(\left( {x \in \mathbb{N}*} \right).\)

Số xe tải loại nhỏ mà đội cần sử dụng theo kế hoạch là \(x + 2\) (xe).

Mỗi xe tải loại lớn vận chuyển được là \(\frac{{15}}{x}\) (tấn).

Mỗi xe tải loại nhỏ theo kế hoạch vận chuyển được là \(\frac{{15}}{{x + 2}}\) (tấn).

Theo bài, mỗi xe tải lớn chở nhiều hơn mỗi xe tải loại nhỏ 2 tấn nên ta có phương trình:

\(\frac{{15}}{x} - \frac{{15}}{{x + 2}} = 2\)

\(15\left( {x + 2} \right) - 15x = 2x\left( {x + 2} \right)\)

\(15x + 30 - 15x = 2{x^2} + 4x\)

\(2{x^2} + 4x - 30 = 0\)

\(x = 3\) hoặc \(x = - 5.\)

Ta thấy chỉ có giá trị \(x = 3\) thỏa mãn điều kiện.

Vậy xe tải loại lớn mà đội vận chuyển cần dùng là \(3\) xe.

2) Diện tích xung quanh của bình đựng nước là:

\({S_4} = 2\pi rh = 2\pi \cdot 4 \cdot 25 = 200\pi \approx 628{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)

Vậy diện tích xung quanh của bình đựng nước khoảng \(628{\rm{\;c}}{{\rm{m}}^2}.\)

Câu 2

Từ điểm \(A\) nằm bên ngoài đường tròn \(\left( O \right),\) kẻ hai tiếp tuyến \(AB,\,\,AC\) với đường tròn \(\left( O \right)\) \((B,\,\,C\) là hai tiếp điểm).

1) Chứng minh tứ giác \(ABOC\) là tứ giác nội tiếp.

2) Vẽ đường kính \(BD\) của đường tròn \(\left( O \right).\) Gọi \(E\) là giao điểm thứ hai của đường thẳng \(AD\) và đường tròn \(\left( O \right).\) Đường thẳng \(BC\) và đường thẳng \(AO\) cắt nhau tại \(H.\) Chứng minh \(A{B^2} = AE \cdot AD = AH \cdot AO\) và \(\widehat {HDO} = \widehat {HBE}.\)

3) Lấy điểm \(M\) thuộc tia đối của tia \(CB.\) Gọi \(N\) là chân đường vuông góc kẻ từ điểm \(M\) đến đường thẳng \(AB.\) Chứng minh đường thẳng \(BE\) đi qua trung điểm của đoạn thẳng \(MN.\)

Xem đáp án

Lời giải

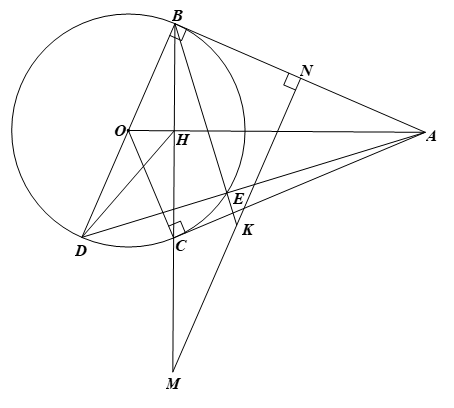
Từ điểm A nằm bên ngoài đường tròn O kẻ hai tiếp tuyến (AB, AC) với đường tròn O B, C là hai tiếp điểm). (ảnh 1)

1) Vì \(AB,\,\,AC\) là các tiếp tuyến của đường tròn \(\left( O \right)\) nên \[\widehat {ABO} = \widehat {ACO} = 90^\circ .\]

Do đó hai điểm \(B,\,\,C\) cùng nằm trên đường tròn đường kính \(AO.\)

Vậy tứ giác \(ABOC\) là tứ giác nội tiếp đường tròn đường kính \(AO.\)

2) ⦁ Ta có \(BD\) là đường kính của đường tròn \(\left( O \right)\) nên \(\widehat {BED} = 90^\circ .\)

Xét \(\Delta ABE\) vuông tại \(E,\) ta có: \(\cos \widehat {BAE} = \frac{{AE}}{{AB}}.\)

Xét \(\Delta ABD\) vuông tại \(B,\) ta có: \(\cos \widehat {BAD} = \frac{{AB}}{{AD}}.\)

Do đó \[\frac{{AE}}{{AB}} = \frac{{AB}}{{AD}}\] hay \(A{B^2} = AE \cdot AD.\)

Lại có \(AB = AC\) (tính chất hai tiếp tuyến \(AB,\,\,AC\) của đường tròn \(\left( O \right)\) cắt nhau tại \(A)\) và \(OB = OC\) nên đường thẳng \(AO\) là trung trực của đoạn thẳng \(BC.\) Do đó \(AO \bot BC.\)

Chứng minh tương tự như trên ta cũng có:

\(\frac{{AB}}{{AO}} = \cos \widehat {BAO} = \cos \widehat {BAH} = \frac{{AH}}{{AB}},\) suy ra \(A{B^2} = AH \cdot AO.\)

Vậy \(A{B^2} = AE \cdot AD = AH \cdot AO.\)

⦁ Chứng minh tương tự như trên, ta cũng có:

\(OH{\rm{\;}} \cdot OA = O{B^2} = O{D^2}\) hay \(\frac{{OD}}{{OA}} = \frac{{OH}}{{OD}}.\)

Xét \(\Delta ODH\) và \(\Delta OAD\) có: \(\widehat {AOD}\) là góc chung và \(\frac{{OD}}{{OA}} = \frac{{OH}}{{OD}}.\)

Do đó (c.g.c). Suy ra \(\widehat {HDO} = \widehat {DAO}\) (hai góc tương ứng). (1)

Ta có \(\widehat {AHB} = \widehat {AEB} = 90^\circ \) nên hai điểm \(H,\,\,E\) cùng nằm trên đường tròn đường kính \(AB.\)

Do đó tứ giác \(ABHE\) nội tiếp đường tròn đường kính \(AB.\)

Suy ra \(\widehat {EBH} = \widehat {EAH}\) (hai góc nội tiếp cùng chắn cung \(EH).\) Hay \(\widehat {HBE} = \widehat {DAO}.\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra \(\widehat {HDO} = \widehat {HBE}.\)

3) Gọi \(K\) là giao điểm của \(BE\) và \(MN.\)

Ta có \(BD\,{\rm{//}}\,MN\) (cùng vuông góc với \(AB)\) nên \(\widehat {DBM} = \widehat {BMN}\) (hai góc so le trong).

Xét \(\Delta BHD\) và \(\Delta MKB\) có \(\widehat {DBH} = \widehat {BMK},\,\,\widehat {BDH} = \widehat {KBM}\)

Do đó (g.g), suy ra \(\frac{{BH}}{{MK}} = \frac{{BD}}{{MB}}.\,\,\,\left( 3 \right)\)

Xét \(\Delta BCD\) và \(\Delta MNB\) có \(\widehat {BCD} = \widehat {MNB} = 90^\circ \) và \(\widehat {CBD} = \widehat {BMN}\)

Do đó (g.g), suy ra \(\frac{{BC}}{{MN}} = \frac{{BD}}{{MB}}.\,\,\,\,\left( 4 \right)\)

Từ (3) và (4) suy ra \(\frac{{BH}}{{MK}} = \frac{{BC}}{{MN}},\) nên \(\frac{{BH}}{{BC}} = \frac{{MK}}{{MN}}.\)

Do \(OA\) là đường trung trực của \(BC\) nên \(H\) là trung điểm của \(BC,\) suy ra \(BH = \frac{1}{2}BC\) hay \(\frac{{BH}}{{BC}} = \frac{1}{2}\) nên \(\frac{{MK}}{{MN}} = \frac{1}{2},\) do đó \(K\) là trung điểm của \(MN.\)

Câu 3