Câu hỏi:
29/08/2024 613Cho parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 4x - m - 1.\)
1) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) khi \(m = 2.\)
2) Tìm giá trị của tham số \(m\) để đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ là \({x_1},\,\,{x_2}\) thỏa mãn giá trị \({x_1},\,\,{x_2}\) bằng độ dài hai cạnh góc vuông của một tam giác vuông có độ dài đường cao ứng với cạnh huyền là \(h = \frac{1}{{\sqrt 5 }}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
1) Với \(m = 2\) thì \(\left( d \right)\) có dạng \(y = 4x - 3.\)
Gọi \(\left( {{x_0};{y_0}} \right)\) là tọa độ giao điểm (nếu có) của \(\left( d \right)\) và \(\left( P \right),\) khi đó ta có:
\({y_0} = x_0^2\) và \({y_0} = 4{x_0} - 3.\)
Suy ra \(x_0^2 = 4{x_0} - 3\) hay \(x_0^2 - 4{x_0} + 3 = 0.\)
Số giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là số nghiệm của phương trình \(x_0^2 - 4{x_0} + 3 = 0.\,\,\,\left( 1 \right)\)
Ta có \(a + b + c = 1 + \left( { - 4} \right) + 3 = 0\) nên phương trình trên có hai nghiệm là \({x_0} = 1;\,\,{x_0} = 3.\)
⦁ Với \({x_0} = 1\) thay vào \({y_0} = x_0^2,\) ta có \({y_0} = {1^2} = 1.\) Suy ra \(A\left( {1;\,\,1} \right).\)
⦁ Với \({x_0} = 3\) thay vào \({y_0} = x_0^2,\) ta có \({y_0} = {3^2} = 9.\) Suy ra \(B\left( {3;\,\,9} \right).\)
Vậy với \(m = 2\) thì toạ độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là \(A\left( {1;\,\,1} \right)\) và \(B\left( {3;\,\,9} \right).\)
2) Gọi \(\left( {{x_0};{y_0}} \right)\) là tọa độ giao điểm (nếu có) của \(\left( d \right)\) và \(\left( P \right),\) khi đó ta có:
\({y_0} = x_0^2\) và \({y_0} = 4{x_0} - m - 1.\)
Suy ra \(x_0^2 = 4{x_0} - m - 1\) hay \(x_0^2 - 4{x_0} + m + 1 = 0.\)
Số giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là số nghiệm của phương trình \(x_0^2 - 4{x_0} + m + 1 = 0.\,\,\,\left( 2 \right)\)
Ta có: \({\rm{\Delta '}} = {\left( { - 2} \right)^2} - \left( {m + 1} \right) = 3 - m.\)
Để \(\left( P \right)\) cắt \(\left( d \right)\) tại 2 điểm phân biệt hoành độ là \({x_1},\,\,{x_2}\) thì phương trình \(\left( 2 \right)\) phải có hai nghiệm phân biệt \({x_1},\,\,{x_2},\) tức là \(\Delta ' > 0,\) suy ra \(3 - m > 0\) nên \(m < 3.\)
Với \(m < 3,\) áp dụng Viète, ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 4}\\{{x_1} \cdot {x_2} = m + 1.}\end{array}} \right.\)
Để \({x_1},\,\,{x_2}\) là độ dài hai cạnh góc vuông của tam giác vuông thì \(\left\{ \begin{array}{l}{x_1} + {x_2} > 0\\{x_1}{x_2} > 0\end{array} \right.,\) suy ra nên \(m > - 1.\)
Kết hợp điều kiện \(m < 3,\) ta được \[ - 1 < m < 3.\]
Chứng minh bổ đề: Cho tam giác vuông có độ dài cạnh huyền là \(a,\) độ dài hai cạnh góc vuông là \(b,\,\,c\) và độ dài đường cao kẻ từ đỉnh đến cạnh huyền bằng \(a.\) Khi đó:
\(\frac{1}{{{h^2}}} = \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}.\)
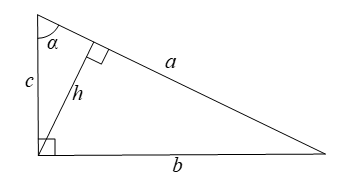
Áp dụng hệ thức đã chứng minh ở bổ đề trên, khi độ dài hai cạnh góc vuông của một tam giác vuông có độ dài đường cao ứng với cạnh huyền là \(h = \frac{1}{{\sqrt 5 }},\) thì ta có:
\(\frac{1}{{x_1^2}} + \frac{1}{{x_2^2}} = \frac{1}{{{{\left( {\frac{1}{{\sqrt 5 }}} \right)}^2}}} = 5\) nên \(\frac{{x_1^2 + x_2^2}}{{{{\left( {{x_1}{x_2}} \right)}^2}}} = 5\)
Suy ra \(x_1^2 + x_2^2 = 5{\left( {{x_1}{x_2}} \right)^2}\)
\({\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 5{\left( {{x_1}{x_2}} \right)^2}\)
Do đó, ta có: \({4^2} - 2\left( {m + 1} \right) = 5{\left( {m + 1} \right)^2}\)
\(5{m^2} + 12m - 9 = 0\)
\(m = - 3\) (không thỏa mãn) hoặc \(m = \frac{3}{5}\) (thỏa mãn).
Vậy với \(m = \frac{3}{5}\) thoả mãn bài toán.
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1) Gọi giá niêm yết của 1 cái bút là \(x\) nghìn đồng \(\left( {x > 0} \right).\)
Vì cô chủ nhiệm mua 40 cái bút nên có 30 cái bút được giảm giá \(20{\rm{\% }}\) so với giá niêm yết
và 10 cái bút được giảm giá \(40{\rm{\% }}\) so với giá niêm yết, khi đó cô chủ nhiệm cần trả số tiền là:
\(30 \cdot \left( {100\% - 20\% } \right)x + 10 \cdot \left( {100\% - 40\% } \right)x = 24x + 6x = 30x\) (nghìn đồng).
Theo bài, cô chủ nhiệm mua 40 cái bút hết \[900{\rm{ }}000\] đồng \( = 900\) nghìn đồng, nên ta có phương trình:
\(30x = 900,\) suy ra \(x = 30\) (nghìn đồng).
Vậy giá niêm yết 1 cái bút là \[30{\rm{ }}000\] đồng.
2) Gọi số bút cô chủ nhiệm mua được là \(a\) chiếc nếu cô có \[1{\rm{ }}260{\rm{ }}000\] đồng \(\left( {a \in {\mathbb{N}^{\rm{*}}}} \right).\)
Theo câu 1) nếu cô mua 40 cái bút thì hết \[900{\rm{ }}000\] đồng nên \(a > 40.\)
Số bút được giảm \(20{\rm{\% }}\) so với giá niêm yết là 30 chiếc, số bút được giảm \(40{\rm{\% }}\) so với giá niêm yết là \(a - 30\) chiếc.
Số tiền cô chủ nhiệm cần trả khi mua \(a\) cái bút là:
\(30 \cdot \left( {100\% - 20\% } \right) \cdot 30 + \left( {a - 30} \right) \cdot \left( {100\% - 40\% } \right) \cdot 30 = 720 + 18\left( {a - 30} \right)\) (nghìn đồng).
Theo bài, tổng số tiền cô mua là \[1{\rm{ }}260{\rm{ }}000\] đồng \( = 1{\rm{ }}260\) nghìn đồng, nên ta có phương trình:
\(720 + 18\left( {a - 30} \right) = 1\,\,260\)
\[18a + 180 = 1\,\,260\]
\[18a = 1\,\,080\]
\[a = 60\] (thỏa mãn).
Vậy nếu có \[1{\rm{ }}260{\rm{ }}000\] đồng cô chủ nhiệm có thể mua được 60 chiếc bút.
Lời giải
1) ⦁ Vì \(CA,CD\) là các tiếp tuyến của đường tròn \(\left( O \right)\), nên \(CA \bot OA\) tại \(A\) và \(AD \bot OD\) tại \(D\) hay \(\widehat {CAO} = 90^\circ ;\,\,\widehat {CDO} = 90^\circ .\)
Do đó hai điểm \(A,\,\,D\) nằm trên đường tròn đường kính \(CO.\)
Vậy tứ giác \(AODC\) nội tiếp được đường tròn đường kính \(CO.\)
2) * Chứng minh \(IC \cdot IO = IH \cdot CO\)
⦁ Do \(C\) là giao của hai tiếp tuyến \(CA,\,\,CD\) của đường tròn \(\left( O \right),\) nên \(OC\) là phân giác của góc \(AOD\) hay \(\widehat {AOI} = \widehat {DOI}.\) Suy ra nên \[\widehat {ADI} = \widehat {IAD}\,\,\,\left( 1 \right)\] (hai góc nội tiếp chắn hai cung bằng nhau của đường tròn \(\left( O \right)).\)
Ta có \(\widehat {CAI} + \widehat {IAO} = 90^\circ \) nên \(\widehat {CAI} = 90^\circ - \widehat {IAO}.\,\,\,\left( 2 \right)\)
Xét \(\Delta OAI\) cân tại \(O\) (do \(OA = OI)\) nên \(\widehat {IAO} = \widehat {AIO} = \frac{{180^\circ - \widehat {AOI}}}{2} = 90^\circ - \frac{1}{2}\widehat {AOI}.\)
Lại có \(\widehat {ADI} = \frac{1}{2}\widehat {AOI}\) (góc nội tiếp và góc ở tâm cùng chắn cung \(AI\) của đường tròn \(\left( O \right)).\)
Do đó \(\widehat {IAO} = 90^\circ - \widehat {ADI}\) hay \(\widehat {ADI} = 90^\circ - \widehat {IAO}.\,\,\,\left( 3 \right)\)
Từ \(\left( 1 \right),\,\,\left( 2 \right)\) và \(\left( 3 \right)\) suy ra \[\widehat {CAI} = \widehat {IAD}\,\,\left( { = \widehat {ADI}} \right)\] hay \(AI\) là phân giác của \(\widehat {CAH}.\)
Xét \(\Delta CAH\) có \[AI\] là phân giác của \(\widehat {CAH}\) nên: \(\frac{{IC}}{{IH}} = \frac{{AC}}{{AH}}.\,\,\,\left( 4 \right)\)
⦁ Ta có \(OA = OD\) và \(CA = CD\) (tính chất hai tiếp tuyến cắt nhau) nên \(OC\) là đường trung trực của \(AD\) hay \(AH \bot OC\)
Xét \(\Delta AHO\) vuông tại \(H,\) ta có \(\sin \widehat {AOH} = \frac{{AH}}{{AO}}.\)
Xét \(\Delta ACO\) vuông tại \(A,\) ta có \(\sin \widehat {AOH} = \sin \widehat {AOC} = \frac{{AC}}{{CO}}.\)
Do đó \(\frac{{AH}}{{AO}} = \frac{{AC}}{{CO}}\) hay \(\frac{{AC}}{{AH}} = \frac{{CO}}{{AO}} = \frac{{CO}}{{OI}}\,\,\,\left( 5 \right)\) (do \(OA = OI)\)
Từ \[\left( 4 \right)\] và \(\left( 5 \right)\) suy ra: \(\frac{{IC}}{{IH}} = \frac{{CO}}{{OI}}\) hay \(IC \cdot OI = IH \cdot CO.\)
* Chứng minh \(\widehat {CKH} = 2\widehat {IAO}\)
Nối \(AK,\) ta có \(\widehat {AKB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) hay \(AK \bot BC.\)
Xét \(\Delta CAK\) và \(\Delta ABC\) có: \(\widehat {AKC} = \widehat {BAC} = 90^\circ \) và \(\widehat {ACB}\) là góc chung
Do đó (g.g), suy ra \(\frac{{CA}}{{CB}} = \frac{{AK}}{{CA}}\) hay \(C{A^2} = CK \cdot CB.\)
Tương tự, ta có (g.g) suy ra \(\frac{{CA}}{{CO}} = \frac{{CH}}{{CA}}\) hay \(C{A^2} = CH \cdot CO.\)
Suy ra \(CK \cdot CB = CH \cdot CO\) nên \(\frac{{CK}}{{CO}} = \frac{{CH}}{{CB}}.\)
Xét \(\Delta CKH\) và \(\Delta COB\) có: \[\widehat {OCB}\] là góc chung và \(\frac{{CK}}{{CO}} = \frac{{CH}}{{CB}}.\)
Do đó (c.g.c), suy ra \(\widehat {CKH} = \widehat {COB}\) (hai góc tương ứng).
Mặt khác \(\widehat {COB} = \widehat {IOB} = 2\widehat {IAB}\) (Góc ở tâm và góc nội tiếp cùng chắn cung \(BI)\)
Suy ra \(\widehat {CKH} = 2\widehat {IAB}\) hay \(\widehat {CKH} = 2 \cdot \widehat {IAO}.\)
3) Ta có \(OM\,{\rm{//}}\,AC\) (cùng vuông góc với \(AB)\)nên \(\widehat {COM} = \widehat {OCA}\) (hai góc so le trong).
Mà \(CO\) là tia phân giác của \(\widehat {ACD}\) (do hai tiếp tuyến \(CA,\,\,CD\) của đường tròn \(\left( O \right)\) cắt nhau tại \(C)\) nên \(\widehat {OCA} = \widehat {OCM}.\)
Do đó \[\widehat {COM} = \widehat {OCM}\] suy ra \[\Delta CMO\] cân tại \(M.\) Từ đó ta có \(MC = MO.\)
Xét \(\Delta ACE\) có \(MO\,{\rm{//}}\,CA\) nên theo hệ quả định lí Thalès, ta có: \[\frac{{CA}}{{MO}} = \frac{{AE}}{{OE}}.\]
Xét \(\Delta ODE\) và \(\Delta MOE\) có: \(\widehat {ODE} = \widehat {MOE} = 90^\circ \) và \(\widehat {OEM}\) là góc chung
Do đó (g.g), suy ra \(\frac{{OE}}{{ME}} = \frac{{OD}}{{MO}}\) hay \(\frac{{OE}}{{OD}} = \frac{{ME}}{{MO}}.\)
Khi đó: \(T = 9 \cdot \frac{{CA}}{{CM}} + \frac{{ME}}{{MO}}\)\( = 9 \cdot \frac{{CA}}{{MO}} + \frac{{ME}}{{MO}}\)\( = 9 \cdot \frac{{AE}}{{OE}} + \frac{{OE}}{{OD}} = 9 \cdot \frac{{OE + OA}}{{OE}} + \frac{{OE}}{{OD}}\)
\( = 9 \cdot \left( {1 + \frac{{OA}}{{OE}}} \right) + \frac{{OE}}{{OA}}\)\( = 9 + \left( {9 \cdot \frac{{OA}}{{OE}} + \frac{{OE}}{{OA}}} \right)\) \[\mathop \ge \limits^{{\rm{B\ST Cauchy}}} \]\[9 + 2\sqrt {9 \cdot \frac{{OA}}{{OE}} \cdot \frac{{OE}}{{OA}}} = 15.\]
Dấu “=" xảy ra khi và chỉ khi \(\frac{{OA}}{{OE}} = \frac{{OE}}{{OA}}\) hay \(9O{A^2} = O{E^2},\) tức là \(OE = 3 \cdot OA = 3R.\)
Dễ dàng chứng minh được (g.g)
Suy ra \(\frac{{OE}}{{CE}} = \frac{{OD}}{{CA}}\) hay \(\frac{{CE}}{{CA}} = \frac{{OE}}{{OD}} = \frac{{3R}}{R} = 3\) hay \(CE = 3CA.\)
Áp dụng định lí Pythagore cho \(\Delta ACE\) vuông tại \(A,\) ta có: \(C{E^2} - C{A^2} = A{E^2}\)
Suy ra \(9 \cdot C{A^2} - C{A^2} = {\left( {AO + OE} \right)^2}\)
Hay \(8C{A^2} = {\left( {R + 3R} \right)^2}\) nên \(8C{A^2} = 16{R^2},\) suy ra \(CA = R\sqrt 2 .\)
Vây điểm \(C\) cách \(A\) một khoảng bằng \(R\sqrt 2 \) thì biểu thức \(T\) đạt giá trị nhỏ nhất bằng \(15.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
50 bài tập Một số yếu tố xác suất có lời giải
-
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
-
Đề thi minh họa (Dự thảo) TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đồng Nai
-
Đề thi thử TS vào 10 (Lần 2 - Tháng 2) năm học 2025 - 2026_Môn Toán_THCS Hoằng Thanh_Tỉnh Thanh Hóa
-
Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Bình Phước
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận