Cho \(a,\,\,b,\,\,c\) là các số thực dương thỏa mãn điều kiện \(a + b + c = 3.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \frac{b}{{{a^2} + 1}} + \frac{c}{{{b^2} + 1}} + \frac{a}{{{c^2} + 1}} + \frac{1}{4}\left( {ab + bc + ca} \right).\)
Cho \(a,\,\,b,\,\,c\) là các số thực dương thỏa mãn điều kiện \(a + b + c = 3.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \frac{b}{{{a^2} + 1}} + \frac{c}{{{b^2} + 1}} + \frac{a}{{{c^2} + 1}} + \frac{1}{4}\left( {ab + bc + ca} \right).\)
Quảng cáo
Trả lời:
Với \(a\) là số thực dương, ta có \[{a^2} + 1 \ge 2a\] nên \(\frac{b}{{{a^2} + 1}} = b - \frac{{{a^2}b}}{{{a^2} + 1}} \ge b - \frac{{{a^2}b}}{{2a}} = b - \frac{{ab}}{2}.\)
Chứng minh tương tự, ta có: \(\frac{c}{{{b^2} + 1}} \ge c - \frac{{bc}}{2}\) và \(\frac{a}{{{c^2} + 1}} \ge a - \frac{{ac}}{2}.\)
Do đó: \(P \ge \left( {a + b + c} \right) - \frac{1}{2}\left( {ab + bc + ca} \right) + \frac{1}{4}\left( {ab + bc + ca} \right) = 3 - \frac{1}{4}\left( {ab + bc + ca} \right)\)
Lại có \(\left( {ab + bc + ca} \right) \le \frac{{{{\left( {a + b + c} \right)}^2}}}{3} = 3\) nên \(P \ge 3 - \frac{1}{4} \cdot 3 = \frac{9}{4}.\)
Dấu “=” xảy ra khi và chỉ khi \(a = b = c = 1.\)
Vậy min \(P = \frac{9}{4}\) khi \(a = b = c = 1.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1) Gọi giá niêm yết của 1 cái bút là \(x\) nghìn đồng \(\left( {x > 0} \right).\)
Vì cô chủ nhiệm mua 40 cái bút nên có 30 cái bút được giảm giá \(20{\rm{\% }}\) so với giá niêm yết
và 10 cái bút được giảm giá \(40{\rm{\% }}\) so với giá niêm yết, khi đó cô chủ nhiệm cần trả số tiền là:
\(30 \cdot \left( {100\% - 20\% } \right)x + 10 \cdot \left( {100\% - 40\% } \right)x = 24x + 6x = 30x\) (nghìn đồng).
Theo bài, cô chủ nhiệm mua 40 cái bút hết \[900{\rm{ }}000\] đồng \( = 900\) nghìn đồng, nên ta có phương trình:
\(30x = 900,\) suy ra \(x = 30\) (nghìn đồng).
Vậy giá niêm yết 1 cái bút là \[30{\rm{ }}000\] đồng.
2) Gọi số bút cô chủ nhiệm mua được là \(a\) chiếc nếu cô có \[1{\rm{ }}260{\rm{ }}000\] đồng \(\left( {a \in {\mathbb{N}^{\rm{*}}}} \right).\)
Theo câu 1) nếu cô mua 40 cái bút thì hết \[900{\rm{ }}000\] đồng nên \(a > 40.\)
Số bút được giảm \(20{\rm{\% }}\) so với giá niêm yết là 30 chiếc, số bút được giảm \(40{\rm{\% }}\) so với giá niêm yết là \(a - 30\) chiếc.
Số tiền cô chủ nhiệm cần trả khi mua \(a\) cái bút là:
\(30 \cdot \left( {100\% - 20\% } \right) \cdot 30 + \left( {a - 30} \right) \cdot \left( {100\% - 40\% } \right) \cdot 30 = 720 + 18\left( {a - 30} \right)\) (nghìn đồng).
Theo bài, tổng số tiền cô mua là \[1{\rm{ }}260{\rm{ }}000\] đồng \( = 1{\rm{ }}260\) nghìn đồng, nên ta có phương trình:
\(720 + 18\left( {a - 30} \right) = 1\,\,260\)
\[18a + 180 = 1\,\,260\]
\[18a = 1\,\,080\]
\[a = 60\] (thỏa mãn).
Vậy nếu có \[1{\rm{ }}260{\rm{ }}000\] đồng cô chủ nhiệm có thể mua được 60 chiếc bút.
Lời giải
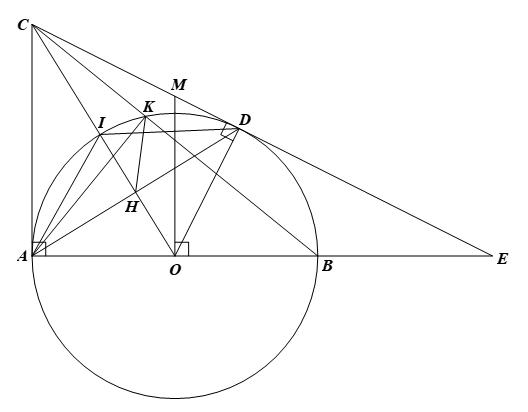
1) ⦁ Vì \(CA,CD\) là các tiếp tuyến của đường tròn \(\left( O \right)\), nên \(CA \bot OA\) tại \(A\) và \(AD \bot OD\) tại \(D\) hay \(\widehat {CAO} = 90^\circ ;\,\,\widehat {CDO} = 90^\circ .\)
Do đó hai điểm \(A,\,\,D\) nằm trên đường tròn đường kính \(CO.\)
Vậy tứ giác \(AODC\) nội tiếp được đường tròn đường kính \(CO.\)
2) * Chứng minh \(IC \cdot IO = IH \cdot CO\)
⦁ Do \(C\) là giao của hai tiếp tuyến \(CA,\,\,CD\) của đường tròn \(\left( O \right),\) nên \(OC\) là phân giác của góc \(AOD\) hay \(\widehat {AOI} = \widehat {DOI}.\) Suy ra nên \[\widehat {ADI} = \widehat {IAD}\,\,\,\left( 1 \right)\] (hai góc nội tiếp chắn hai cung bằng nhau của đường tròn \(\left( O \right)).\)
Ta có \(\widehat {CAI} + \widehat {IAO} = 90^\circ \) nên \(\widehat {CAI} = 90^\circ - \widehat {IAO}.\,\,\,\left( 2 \right)\)
Xét \(\Delta OAI\) cân tại \(O\) (do \(OA = OI)\) nên \(\widehat {IAO} = \widehat {AIO} = \frac{{180^\circ - \widehat {AOI}}}{2} = 90^\circ - \frac{1}{2}\widehat {AOI}.\)
Lại có \(\widehat {ADI} = \frac{1}{2}\widehat {AOI}\) (góc nội tiếp và góc ở tâm cùng chắn cung \(AI\) của đường tròn \(\left( O \right)).\)
Do đó \(\widehat {IAO} = 90^\circ - \widehat {ADI}\) hay \(\widehat {ADI} = 90^\circ - \widehat {IAO}.\,\,\,\left( 3 \right)\)
Từ \(\left( 1 \right),\,\,\left( 2 \right)\) và \(\left( 3 \right)\) suy ra \[\widehat {CAI} = \widehat {IAD}\,\,\left( { = \widehat {ADI}} \right)\] hay \(AI\) là phân giác của \(\widehat {CAH}.\)
Xét \(\Delta CAH\) có \[AI\] là phân giác của \(\widehat {CAH}\) nên: \(\frac{{IC}}{{IH}} = \frac{{AC}}{{AH}}.\,\,\,\left( 4 \right)\)
⦁ Ta có \(OA = OD\) và \(CA = CD\) (tính chất hai tiếp tuyến cắt nhau) nên \(OC\) là đường trung trực của \(AD\) hay \(AH \bot OC\)
Xét \(\Delta AHO\) vuông tại \(H,\) ta có \(\sin \widehat {AOH} = \frac{{AH}}{{AO}}.\)
Xét \(\Delta ACO\) vuông tại \(A,\) ta có \(\sin \widehat {AOH} = \sin \widehat {AOC} = \frac{{AC}}{{CO}}.\)
Do đó \(\frac{{AH}}{{AO}} = \frac{{AC}}{{CO}}\) hay \(\frac{{AC}}{{AH}} = \frac{{CO}}{{AO}} = \frac{{CO}}{{OI}}\,\,\,\left( 5 \right)\) (do \(OA = OI)\)
Từ \[\left( 4 \right)\] và \(\left( 5 \right)\) suy ra: \(\frac{{IC}}{{IH}} = \frac{{CO}}{{OI}}\) hay \(IC \cdot OI = IH \cdot CO.\)
* Chứng minh \(\widehat {CKH} = 2\widehat {IAO}\)
Nối \(AK,\) ta có \(\widehat {AKB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) hay \(AK \bot BC.\)
Xét \(\Delta CAK\) và \(\Delta ABC\) có: \(\widehat {AKC} = \widehat {BAC} = 90^\circ \) và \(\widehat {ACB}\) là góc chung
Do đó (g.g), suy ra \(\frac{{CA}}{{CB}} = \frac{{AK}}{{CA}}\) hay \(C{A^2} = CK \cdot CB.\)
Tương tự, ta có (g.g) suy ra \(\frac{{CA}}{{CO}} = \frac{{CH}}{{CA}}\) hay \(C{A^2} = CH \cdot CO.\)
Suy ra \(CK \cdot CB = CH \cdot CO\) nên \(\frac{{CK}}{{CO}} = \frac{{CH}}{{CB}}.\)
Xét \(\Delta CKH\) và \(\Delta COB\) có: \[\widehat {OCB}\] là góc chung và \(\frac{{CK}}{{CO}} = \frac{{CH}}{{CB}}.\)
Do đó (c.g.c), suy ra \(\widehat {CKH} = \widehat {COB}\) (hai góc tương ứng).
Mặt khác \(\widehat {COB} = \widehat {IOB} = 2\widehat {IAB}\) (Góc ở tâm và góc nội tiếp cùng chắn cung \(BI)\)
Suy ra \(\widehat {CKH} = 2\widehat {IAB}\) hay \(\widehat {CKH} = 2 \cdot \widehat {IAO}.\)
3) Ta có \(OM\,{\rm{//}}\,AC\) (cùng vuông góc với \(AB)\)nên \(\widehat {COM} = \widehat {OCA}\) (hai góc so le trong).
Mà \(CO\) là tia phân giác của \(\widehat {ACD}\) (do hai tiếp tuyến \(CA,\,\,CD\) của đường tròn \(\left( O \right)\) cắt nhau tại \(C)\) nên \(\widehat {OCA} = \widehat {OCM}.\)
Do đó \[\widehat {COM} = \widehat {OCM}\] suy ra \[\Delta CMO\] cân tại \(M.\) Từ đó ta có \(MC = MO.\)
Xét \(\Delta ACE\) có \(MO\,{\rm{//}}\,CA\) nên theo hệ quả định lí Thalès, ta có: \[\frac{{CA}}{{MO}} = \frac{{AE}}{{OE}}.\]
Xét \(\Delta ODE\) và \(\Delta MOE\) có: \(\widehat {ODE} = \widehat {MOE} = 90^\circ \) và \(\widehat {OEM}\) là góc chung
Do đó (g.g), suy ra \(\frac{{OE}}{{ME}} = \frac{{OD}}{{MO}}\) hay \(\frac{{OE}}{{OD}} = \frac{{ME}}{{MO}}.\)
Khi đó: \(T = 9 \cdot \frac{{CA}}{{CM}} + \frac{{ME}}{{MO}}\)\( = 9 \cdot \frac{{CA}}{{MO}} + \frac{{ME}}{{MO}}\)\( = 9 \cdot \frac{{AE}}{{OE}} + \frac{{OE}}{{OD}} = 9 \cdot \frac{{OE + OA}}{{OE}} + \frac{{OE}}{{OD}}\)
\( = 9 \cdot \left( {1 + \frac{{OA}}{{OE}}} \right) + \frac{{OE}}{{OA}}\)\( = 9 + \left( {9 \cdot \frac{{OA}}{{OE}} + \frac{{OE}}{{OA}}} \right)\) \[\mathop \ge \limits^{{\rm{B\ST Cauchy}}} \]\[9 + 2\sqrt {9 \cdot \frac{{OA}}{{OE}} \cdot \frac{{OE}}{{OA}}} = 15.\]
Dấu “=" xảy ra khi và chỉ khi \(\frac{{OA}}{{OE}} = \frac{{OE}}{{OA}}\) hay \(9O{A^2} = O{E^2},\) tức là \(OE = 3 \cdot OA = 3R.\)
Dễ dàng chứng minh được (g.g)
Suy ra \(\frac{{OE}}{{CE}} = \frac{{OD}}{{CA}}\) hay \(\frac{{CE}}{{CA}} = \frac{{OE}}{{OD}} = \frac{{3R}}{R} = 3\) hay \(CE = 3CA.\)
Áp dụng định lí Pythagore cho \(\Delta ACE\) vuông tại \(A,\) ta có: \(C{E^2} - C{A^2} = A{E^2}\)
Suy ra \(9 \cdot C{A^2} - C{A^2} = {\left( {AO + OE} \right)^2}\)
Hay \(8C{A^2} = {\left( {R + 3R} \right)^2}\) nên \(8C{A^2} = 16{R^2},\) suy ra \(CA = R\sqrt 2 .\)
Vây điểm \(C\) cách \(A\) một khoảng bằng \(R\sqrt 2 \) thì biểu thức \(T\) đạt giá trị nhỏ nhất bằng \(15.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.