Trên đường tròn (O) bán kính R, lấy các điểm A, B, C, D sao cho sđAB⏜=60°, sđBC⏜=90°, sđCD⏜=120° (Hình 7). a) Xác định tâm và tính theo R bán kính đường tròn ngoại tiếp của các tam giác OAB, OBC, OAD...

Câu hỏi:

13/09/2024 2,322

Trên đường tròn (O) bán kính R, lấy các điểm A, B, C, D sao cho $s đ \overset{⏜}{A B} = 60 °, s đ \overset{⏜}{B C} = 90 °, s đ \overset{⏜}{C D} = 120 °$ (Hình 7).

a) Xác định tâm và tính theo R bán kính đường tròn ngoại tiếp của các tam giác OAB, OBC, OAD, ODC.

b) Gọi I là giao điểm của AC và BD. Tính bán kính đường tròn ngoại tiếp của các tam giác IAB, IBC, IAD, IDC.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 9 Cánh diều Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

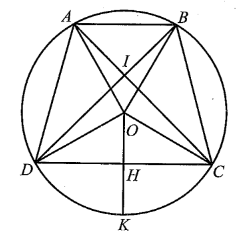
Trên đường tròn (O) bán kính R, lấy các điểm A, B, C, D sao cho sđ AB =60 độ, sđ BC =90 độ (ảnh 2)

a) ⦁ Gọi G là trọng tâm của tam giác OAB.

Do A, B thuộc đường tròn (O) nên OA = OB = R.

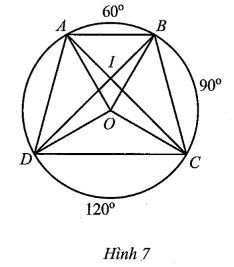
Lại có $s đ \overset{⏜}{A B} = 60 °$ nên $\hat{A O B} = 60 °$ (góc ở tâm chắn cung AB của đường tròn (O)).

Do đó, tam giác OAB là tam giác đều với cạnh AB = OA = OB = R nên có tâm đường tròn ngoại tiếp là G và bán kính đường tròn ngoại tiếp là $\frac{R \sqrt{3}}{3}$ .

⦁ Do $s đ \overset{⏜}{B C} = 90 °$ nên $\hat{B O C} = 90 °$ (góc ở tâm chắn cung BC của đường tròn (O)).

Do đó tam giác OBC vuông tại O, theo định lí Pythagore, ta có:

BC² = OB² + OC²

Suy ra $B C = \sqrt{O B^{2} + O C^{2}} = \sqrt{R^{2} + R^{2}} = R \sqrt{2}$ nên tâm, bán kính đường tròn ngoại tiếp của ∆OBC lần lượt là trung điểm E của BC và $\frac{R \sqrt{2}}{2}$ .

⦁ Tương tự tâm, bán kính đường tròn ngoại tiếp tam giác OAD lần lượt là trung điểm F của AD và $\frac{R \sqrt{2}}{2}$ .

⦁ Gọi H là trung điểm của DC và giao điểm của tia OH và cung nhỏ CD là K.

Do $s đ \overset{⏜}{C D} = 120^{°}$ nên $\hat{D O C} = 120 °$ (góc nội tiếp chắn cung DC của đường tròn (O)).

Trong tam giác ODC cân tại O có OH là trung tuyến nên đồng thời là phân giác của $\hat{D O C}$ .

Suy ra $\hat{D O H} = \hat{C O H} = \frac{1}{2} \hat{D O C} = \frac{1}{2} \cdot 120 ° = 60 °$ .

Lại có OD = OK = OC nên ∆DOK, ∆COK là tam giác đều.

Suy ra KD = KO = KC = R.

Vậy tâm và bán kính đường tròn ngoại tiếp tam giác ODC lần lượt là K và R.

b) Xét ∆OHC vuông tại H có $H C = O C \cdot \sin \hat{C O H} = R \cdot \sin 60 ° = \frac{R \sqrt{3}}{2}$ .

Suy ra $D C = 2 H C = 2 \cdot \frac{R \sqrt{3}}{2} = R \sqrt{3}$ .

Xét đường tròn (O) có $\hat{C A B} = \frac{1}{2} s đ \overset{⏜}{C B} = \frac{1}{2} \cdot 90 ° = 45 °$ (góc nội tiếp chắn cung BC).

Ta có $s đ \overset{⏜}{A B} + s đ \overset{⏜}{B C} + s đ \overset{⏜}{C D} + s đ \overset{⏜}{D A} = 360 °$

Suy ra $s đ \overset{⏜}{D A} = 360 ° - s đ \overset{⏜}{A B} - s đ \overset{⏜}{B C} - s đ \overset{⏜}{C D} = 360 ° - 60 ° - 90 ° - 120 ° = 90 °$

Khi đó, $\hat{D B A} = \frac{1}{2} s đ \overset{⏜}{D A} = \frac{1}{2} \cdot 90 ° = 45 °$ (góc nội tiếp chắn cung DA).

Do đó $\hat{C A B} = \hat{D B A} = 45 °$ .

Xét ∆ABI có: $\hat{I A B} + \hat{I B A} + \hat{A I B} = 180 °$ .

Suy ra $\hat{A I B} = 180 ° - \hat{I A B} - \hat{I B A} = 180 ° - 45 ° - 45 ° = 90 °$ .

Hay AC vuông góc với BD.

Do đó ∆IAB vuông tại I, ∆IAD vuông tại I, ∆IBC vuông tại I, ∆IDC vuông tại I.

Mặt khác, AB = R, $B C = A D = R \sqrt{2}$ (chứng minh ở câu a) và $D C = R \sqrt{3}$ do đó bán kính đường tròn ngoại tiếp của các tam giác IAB, IBC, IAD, IDC lần lượt là: $\frac{R}{2}, \frac{R \sqrt{2}}{2}, \frac{R \sqrt{2}}{2}, \frac{R \sqrt{3}}{2} .$

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm phân biệt A, B. Đường thẳng AO cắt (O) và (O’) lần lượt tại hai điểm C, E (khác điểm A). Đường thẳng AO’ cắt (O) và (O’) lần lượt tại hai điểm D, F (khác điểm A). Chứng minh:

a) C, B, F thẳng hàng;

b) Bốn điểm C, D, E, F cùng nằm trên một đường tròn;

c) A là tâm đường tròn nội tiếp tam giác BDE.

Xem đáp án

Lời giải

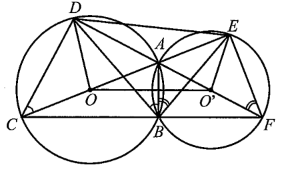
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm phân biệt A, B. Đường thẳng AO cắt (O) và (O’) lần lượt (ảnh 1)

a) Xét đường tròn (O) có AC là đường kính nên $\hat{A B C} = 90 °$ (góc nội tiếp chắn nửa đường tròn (O)).

Xét đường tròn (O’) có AF là đường kính nên $\hat{A B F} = 90 °$ (góc nội tiếp chắn nửa đường tròn (O’)).

Do đó $\hat{A B C} + \hat{A B F} = 90 ° + 90 ° = 180 °$ hay $\hat{C B F} = 180 °$ .

Suy ra C, B, F thẳng hàng.

b) Xét đường tròn (O) có AC là đường kính nên $\hat{A D C} = 90 °$ (góc nội tiếp chắn nửa đường tròn (O)).

Xét đường tròn (O’) có AF là đường kính nên $\hat{A E F} = 90 °$ (góc nội tiếp chắn nửa đường tròn (O’)).

Do đó $\hat{F D C} = \hat{C E F} = 90 °$ nên hai điểm D, E nằm trên đường tròn đường kính CF.

Vậy bốn điểm C, D, E, F cùng nằm trên một đường tròn đường kính CF.

c) Ta có $\hat{D C A} = \hat{D B A}$ (hai góc nội tiếp cùng chắn cung DA của đường tròn (O)).

Tương tự $\hat{A B E} = \hat{A F E}$ và $\hat{D C E} = \hat{D F E}$ .

Suy ra $\hat{A B E} = \hat{D B A}$ do đó BA là phân giác của góc DBE.

Tương tự, DA là phân giác của góc BDE.

Suy ra A là tâm đường tròn nội tiếp tam giác BDE.

Câu 2

Cho tam giác ABC vuông tại A có AB = 6, AC = 8, bán kính đường tròn nội tiếp là r, bán kính đường tròn ngoại tiếp là R. Tính $\frac{r}{R}$

Xem đáp án

Lời giải

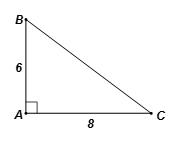
Cho tam giác ABC vuông tại A có AB = 6, AC = 8, bán kính đường tròn nội tiếp là r, bán kính đường tròn ngoại tiếp (ảnh 1)

Tam giác ABC vuông tại A, theo định lí Pythagore, ta có:

BC² = AB² + AC² = 6² + 8² = 100.

Suy ra $B C = \sqrt{100} = 10$

Do đó bán kính đường tròn ngoại tiếp tam giác ABC là $R = \frac{B C}{2} = \frac{10}{2} = 5$ .

Lại có $r = \frac{A B + A C - B C}{2}$ (theo kết quả của Ví dụ 4, trang 83, SBT Toán 9, Tập một)

Suy ra $r = \frac{A B + A C - B C}{2}$ $= \frac{6 + 8 - 10}{2} = \frac{4}{2} = 2$ .

Do đó $\frac{r}{R} = \frac{2}{5}$ .

Câu 3

Tìm phát biểu đúng trong các phát biểu sau:

a) Tâm đường tròn ngoại tiếp tam giác là giao điểm ba đường phân giác của tam giác đó.

b) Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó.

c) Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tam giác ABC cân tại A, có O, I lần lượt là tâm các đường tròn ngoại tiếp và đường tròn nội tiếp tam giác ABC.

a) Chứng minh rằng:

– Ba điểm A, O, I cùng thuộc một đường thẳng;

– Đường thẳng OA vuông góc với BC và đi qua điểm chính giữa D (khác điểm A) của cung BC.

b) Cho BC = 24 cm, AC = 20 cm. Tính độ dài bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho tam giác nhọn ABC. Các đường cao BE, CD của tam giác ABC cắt nhau tại K. Tìm tâm đường tròn ngoại tiếp mỗi tam giác sau:

a) Tam giác BDE;

b) Tam giác DEC;

c) Tam giác ADE.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho tam giác đều ABC nội tiếp đường tròn tâm O, bán kính R.

a) Chứng minh rằng O cũng là tâm đường tròn nội tiếp tam giác ABC.

b) Vẽ tam giác IJK ngoại tiếp đường tròn (O; R) với JK // BC, IJ // AC, IK // AB. Chứng minh tam giác IJK đều.

c) Gọi R’ là bán kính của đường tròn ngoại tiếp tam giác IJK và r là bán kính của đường tròn nội tiếp tam giác ABC. Tính $\frac{r}{R'}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Cho tam giác ABC vuông tại A có AB = 6, AC = 8, bán kính đường tròn nội tiếp là r, bán kính đường tròn ngoại tiếp là R. Tính rR

Cho tam giác nhọn ABC. Các đường cao BE, CD của tam giác ABC cắt nhau tại K. Tìm tâm đường tròn ngoại tiếp mỗi tam giác sau: a) Tam giác BDE; b) Tam giác DEC; c) Tam giác ADE.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho tam giác ABC vuông tại A có AB = 6, AC = 8, bán kính đường tròn nội tiếp là r, bán kính đường tròn ngoại tiếp là R. Tính $\frac{r}{R}$

Cho tam giác nhọn ABC. Các đường cao BE, CD của tam giác ABC cắt nhau tại K. Tìm tâm đường tròn ngoại tiếp mỗi tam giác sau:

a) Tam giác BDE;

b) Tam giác DEC;

c) Tam giác ADE.