Câu hỏi:
19/09/2024 1,520
Chi hai vectơ \(\overrightarrow u ,\overrightarrow v \) thỏa mãn \(\left| {\overrightarrow u } \right|\) = 2, \(\left| {\overrightarrow v } \right|\) = 1 và \(\left( {\overrightarrow u ,\overrightarrow v } \right)\) = 60°. Tính góc giữa hai vectơ \(\overrightarrow v \) và \(\overrightarrow u - \overrightarrow v \).
Chi hai vectơ \(\overrightarrow u ,\overrightarrow v \) thỏa mãn \(\left| {\overrightarrow u } \right|\) = 2, \(\left| {\overrightarrow v } \right|\) = 1 và \(\left( {\overrightarrow u ,\overrightarrow v } \right)\) = 60°. Tính góc giữa hai vectơ \(\overrightarrow v \) và \(\overrightarrow u - \overrightarrow v \).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vẽ tam giác đều ABC và M là trung điểm BC.
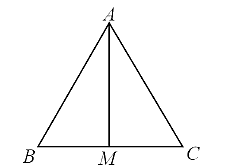
Ta chọn \(\overrightarrow u = \overrightarrow {BA} \), \(\overrightarrow v = \overrightarrow {BM} \) thỏa mãn giá thiết bài toán.
Suy ra \(\overrightarrow u - \overrightarrow v = \overrightarrow {BA} - \overrightarrow {BM} = \overrightarrow {MA} \).
Khi đó, \(\left( {\overrightarrow v ,\overrightarrow u - \overrightarrow v } \right) = \left( {\overrightarrow {BM} ,\overrightarrow {MA} } \right)\) = 90°.
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC có A(0; 0; 1), B(−1; −2; 0), C(2; 1; −1). Tìm tọa độ chân đường cao H hạ từ A xuống BC.
Cho tam giác ABC có A(0; 0; 1), B(−1; −2; 0), C(2; 1; −1). Tìm tọa độ chân đường cao H hạ từ A xuống BC.
Xem đáp án »
19/09/2024
18,410
Câu 2:
Cho ba điểm A(1; 1;1 ), B(−1; 1; 0) và C(3; 1; −1). Gọi M(a; b; c) là điểm thuộc mặt phẳng (Oxz) và cách đều ba điểm A, B, C. Tính tổng a + b + c.
Cho ba điểm A(1; 1;1 ), B(−1; 1; 0) và C(3; 1; −1). Gọi M(a; b; c) là điểm thuộc mặt phẳng (Oxz) và cách đều ba điểm A, B, C. Tính tổng a + b + c.
Xem đáp án »
19/09/2024
10,669
Câu 3:
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 2\sqrt 3 \), \(\left| {\overrightarrow b } \right|\) = 3 và \(\left( {\overrightarrow a ,\overrightarrow b } \right)\) = 30°. Tính độ dài của vectơ \(3\overrightarrow a - 2\overrightarrow b \).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 2\sqrt 3 \), \(\left| {\overrightarrow b } \right|\) = 3 và \(\left( {\overrightarrow a ,\overrightarrow b } \right)\) = 30°. Tính độ dài của vectơ \(3\overrightarrow a - 2\overrightarrow b \).
Xem đáp án »
19/09/2024
9,041
Câu 4:
Trong không gian Oxyz được thiết lập tại một sân bay, người ta ghi nhận hai máy bay đang bay đến với các vectơ vận tốc \(\overrightarrow u \) = (90; −80; −120), \(\overrightarrow v \) = (60; −50; −60).
Tính góc giữa hai vectơ vận tốc nói trên (kết quả làm tròn đến hàng phần mười của độ).
Trong không gian Oxyz được thiết lập tại một sân bay, người ta ghi nhận hai máy bay đang bay đến với các vectơ vận tốc \(\overrightarrow u \) = (90; −80; −120), \(\overrightarrow v \) = (60; −50; −60).
Tính góc giữa hai vectơ vận tốc nói trên (kết quả làm tròn đến hàng phần mười của độ).
Xem đáp án »
19/09/2024
5,615
Câu 5:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2.
a) \(\overrightarrow {AB} = \overrightarrow {C'D'} \).
b) \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {D'C'} \).
c) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
d) \(\overrightarrow {AC} .\overrightarrow {AD'} = 8\).
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2.
a) \(\overrightarrow {AB} = \overrightarrow {C'D'} \).
b) \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {D'C'} \).
c) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
d) \(\overrightarrow {AC} .\overrightarrow {AD'} = 8\).
Xem đáp án »
19/09/2024
4,309
Câu 6:
Cho ba vectơ \(\overrightarrow a \) = (1; 0; −2), \(\overrightarrow b \) = (−2; 1; 3) và \(\overrightarrow c \) = (−4; 3; 5). Tìm hai số thực m, n sao cho \(m\overrightarrow a + n\overrightarrow b = \overrightarrow c \).
Cho ba vectơ \(\overrightarrow a \) = (1; 0; −2), \(\overrightarrow b \) = (−2; 1; 3) và \(\overrightarrow c \) = (−4; 3; 5). Tìm hai số thực m, n sao cho \(m\overrightarrow a + n\overrightarrow b = \overrightarrow c \).
Xem đáp án »
19/09/2024
3,451
Câu 7:
Cho hai vectơ \(\overrightarrow u \) = (2; −1; 2), \(\overrightarrow v \) thỏa mãn \(\left| {\overrightarrow v } \right|\) = 1 và \(\left| {\overrightarrow u - \overrightarrow v } \right|\) = 4. Tính độ dài của vectơ \(\overrightarrow u + \overrightarrow v \).
Cho hai vectơ \(\overrightarrow u \) = (2; −1; 2), \(\overrightarrow v \) thỏa mãn \(\left| {\overrightarrow v } \right|\) = 1 và \(\left| {\overrightarrow u - \overrightarrow v } \right|\) = 4. Tính độ dài của vectơ \(\overrightarrow u + \overrightarrow v \).
Xem đáp án »
19/09/2024
2,830
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận