Câu hỏi:
19/09/2024 1,276
Để nghiên cứu mô hình mạng tinh thể than chì, một nhà hóa học đã thiết lập một hệ tọa độ Oxyz như Hình 2 (đơn vị: nm). Cho biết ABCDEF có dạng lục giác đều.
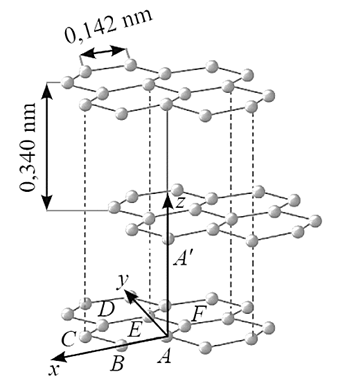
Tìm tọa độ các điểm A, B, C, E, A'.
Để nghiên cứu mô hình mạng tinh thể than chì, một nhà hóa học đã thiết lập một hệ tọa độ Oxyz như Hình 2 (đơn vị: nm). Cho biết ABCDEF có dạng lục giác đều.
Tìm tọa độ các điểm A, B, C, E, A'.
Quảng cáo
Trả lời:
Giải bởi Vietjack
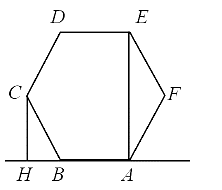
Ta có: AH = \(\frac{3}{2}AB = 0,213\) (nm).
\(CH = \frac{{AB\sqrt 3 }}{2}\) ≈ 0,123 (nm).
AE = \(AB\sqrt 3 \) ≈ 0,246 (nm).
Suy ra A(0; 0; 0), B(0,142; 0; 0), C(0,213; 0,213; 0), E(0; 0,246; 0), A'(0; 0; 0,340).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC có A(0; 0; 1), B(−1; −2; 0), C(2; 1; −1). Tìm tọa độ chân đường cao H hạ từ A xuống BC.
Cho tam giác ABC có A(0; 0; 1), B(−1; −2; 0), C(2; 1; −1). Tìm tọa độ chân đường cao H hạ từ A xuống BC.
Xem đáp án »
19/09/2024
19,079
Câu 2:
Cho ba điểm A(1; 1;1 ), B(−1; 1; 0) và C(3; 1; −1). Gọi M(a; b; c) là điểm thuộc mặt phẳng (Oxz) và cách đều ba điểm A, B, C. Tính tổng a + b + c.
Cho ba điểm A(1; 1;1 ), B(−1; 1; 0) và C(3; 1; −1). Gọi M(a; b; c) là điểm thuộc mặt phẳng (Oxz) và cách đều ba điểm A, B, C. Tính tổng a + b + c.
Xem đáp án »
19/09/2024
10,848
Câu 3:
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 2\sqrt 3 \), \(\left| {\overrightarrow b } \right|\) = 3 và \(\left( {\overrightarrow a ,\overrightarrow b } \right)\) = 30°. Tính độ dài của vectơ \(3\overrightarrow a - 2\overrightarrow b \).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 2\sqrt 3 \), \(\left| {\overrightarrow b } \right|\) = 3 và \(\left( {\overrightarrow a ,\overrightarrow b } \right)\) = 30°. Tính độ dài của vectơ \(3\overrightarrow a - 2\overrightarrow b \).
Xem đáp án »
19/09/2024
10,416
Câu 4:
Trong không gian Oxyz được thiết lập tại một sân bay, người ta ghi nhận hai máy bay đang bay đến với các vectơ vận tốc \(\overrightarrow u \) = (90; −80; −120), \(\overrightarrow v \) = (60; −50; −60).
Tính góc giữa hai vectơ vận tốc nói trên (kết quả làm tròn đến hàng phần mười của độ).
Trong không gian Oxyz được thiết lập tại một sân bay, người ta ghi nhận hai máy bay đang bay đến với các vectơ vận tốc \(\overrightarrow u \) = (90; −80; −120), \(\overrightarrow v \) = (60; −50; −60).
Tính góc giữa hai vectơ vận tốc nói trên (kết quả làm tròn đến hàng phần mười của độ).
Xem đáp án »
19/09/2024
5,990
Câu 5:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2.
a) \(\overrightarrow {AB} = \overrightarrow {C'D'} \).
b) \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {D'C'} \).
c) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
d) \(\overrightarrow {AC} .\overrightarrow {AD'} = 8\).
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2.
a) \(\overrightarrow {AB} = \overrightarrow {C'D'} \).
b) \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {D'C'} \).
c) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
d) \(\overrightarrow {AC} .\overrightarrow {AD'} = 8\).
Xem đáp án »
19/09/2024
4,711
Câu 6:
Cho ba vectơ \(\overrightarrow a \) = (1; 0; −2), \(\overrightarrow b \) = (−2; 1; 3) và \(\overrightarrow c \) = (−4; 3; 5). Tìm hai số thực m, n sao cho \(m\overrightarrow a + n\overrightarrow b = \overrightarrow c \).
Cho ba vectơ \(\overrightarrow a \) = (1; 0; −2), \(\overrightarrow b \) = (−2; 1; 3) và \(\overrightarrow c \) = (−4; 3; 5). Tìm hai số thực m, n sao cho \(m\overrightarrow a + n\overrightarrow b = \overrightarrow c \).
Xem đáp án »
19/09/2024
3,562
Câu 7:
Cho hai vectơ \(\overrightarrow u \) = (2; −1; 2), \(\overrightarrow v \) thỏa mãn \(\left| {\overrightarrow v } \right|\) = 1 và \(\left| {\overrightarrow u - \overrightarrow v } \right|\) = 4. Tính độ dài của vectơ \(\overrightarrow u + \overrightarrow v \).
Cho hai vectơ \(\overrightarrow u \) = (2; −1; 2), \(\overrightarrow v \) thỏa mãn \(\left| {\overrightarrow v } \right|\) = 1 và \(\left| {\overrightarrow u - \overrightarrow v } \right|\) = 4. Tính độ dài của vectơ \(\overrightarrow u + \overrightarrow v \).
Xem đáp án »
19/09/2024
2,894
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận