Câu hỏi:
24/09/2024 739
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(\left( {{{\rm{P}}_1}} \right):3{\rm{x}} + 4{\rm{y}} + 7 = 0\) và \(\left( {{P_2}} \right):5x + 12z + 17 = 0.\)
a) Mặt phẳng \(\left( {{{\rm{P}}_1}} \right)\) có một vectơ pháp tuyến với tọa độ là \((3;4;7).\)
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(\left( {{{\rm{P}}_1}} \right):3{\rm{x}} + 4{\rm{y}} + 7 = 0\) và \(\left( {{P_2}} \right):5x + 12z + 17 = 0.\)
a) Mặt phẳng \(\left( {{{\rm{P}}_1}} \right)\) có một vectơ pháp tuyến với tọa độ là \((3;4;7).\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Mặt phẳng (P1) có một vectơ pháp tuyến với toạ độ là \((3;4;0)\), không phải \((3;4;7).\)
=> Sai
Câu hỏi cùng đoạn
Câu 2:
b) Mặt phẳng \(\left( {{{\rm{P}}_2}} \right)\) có một vectơ pháp tuyến với tọa độ là \((5;12;17).\)
b) Mặt phẳng \(\left( {{{\rm{P}}_2}} \right)\) có một vectơ pháp tuyến với tọa độ là \((5;12;17).\)
Lời giải của GV VietJack
b) Mặt phẳng (P2) có một vectơ pháp tuyến với toạ độ là \((5;0;12)\), không phải \((5;12;17).\)
=> Sai
Câu 3:
c) Tích vô hướng của hai vectơ với tọa độ \((3;4;0)\) và \((5;0;12)\) bằng 15.
c) Tích vô hướng của hai vectơ với tọa độ \((3;4;0)\) và \((5;0;12)\) bằng 15.
Lời giải của GV VietJack
c) Tích vô hướng của hai vectơ với toạ độ \((3;4;0)\) và \((5;0;12)\) bằng \(3 \cdot 5 + 4.0 + 0.12 = 15.\)
=> Đúng
Câu 4:
d) Góc giữa hai mặt phẳng \(\left( {{{\rm{P}}_1}} \right)\) và \(\left( {{{\rm{P}}_2}} \right)\) (làm tròn đến hàng đơn vị của độ) bằng \({77^o }.\)
d) Góc giữa hai mặt phẳng \(\left( {{{\rm{P}}_1}} \right)\) và \(\left( {{{\rm{P}}_2}} \right)\) (làm tròn đến hàng đơn vị của độ) bằng \({77^o }.\)
Lời giải của GV VietJack
d) Côsin góc giữa hai mặt phẳng (P1) và (P2) bằng \(\frac{{15}}{{\sqrt {{3^2} + {4^2} + {0^2}} \cdot \sqrt {{5^2} + {0^2} + {{12}^2}} }} = \frac{3}{{13}}.\)
Góc giữa hai mặt phẳng (P1) và (P2) (làm tròn đến hàng đơn vị của độ) bằng \({77^o}.\)
=> Đúng
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp số: 139.
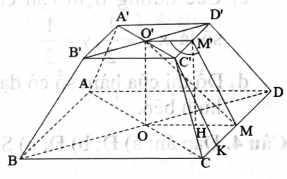
\({\rm{MK}} = \frac{{{{\rm{C}}^\prime }{{\rm{D}}^\prime }}}{2} = 4(\;{\rm{m}})\)\({\rm{CK}} = {\rm{MC}} - {\rm{MK}} = 7 - 4 = 3(\;{\rm{m}}).\)
\({{\rm{C}}^\prime }{{\rm{K}}^2} = {\rm{C}}{{\rm{C}}^{\prime 2}} - {\rm{C}}{{\rm{K}}^2} = {5^2} - {3^2} = 16\),
\({{\rm{C}}^\prime }{\rm{K}} = 4(\;{\rm{m}}).\)
\({\rm{M}}{{\rm{M}}^\prime } = {{\rm{C}}^\prime }{\rm{K}} = 4(\;{\rm{m}}).\)
\({\rm{MH}} = {\rm{OM}} - {\rm{OH}} = 7 - 4 = 3(\;{\rm{m}}).\)
\(\cos \widehat {{\rm{M}}{{\rm{M}}^\prime }{{\rm{O}}^\prime }} = - \cos \widehat {{\rm{HM}}{{\rm{M}}^\prime }} = - \frac{{{\rm{HM}}}}{{{\rm{M}}{{\rm{M}}^\prime }}} = - \frac{3}{4}\),
\(\widehat {{\rm{M}}{{\rm{M}}^\prime }{{\rm{O}}^\prime }} \approx {139^o }.\)
Lời giải
Đáp số: 30.
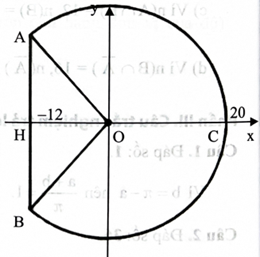
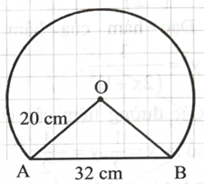
Chọn hệ trục toạ độ như hình vẽ, đơn vị của mỗi trục là 1 cm. Đường tròn chứa cung tròn lớn ACB có phương trình \({{\rm{x}}^2} + {{\rm{y}}^2} = 400.\)
\({\rm{AH}} = {\rm{BH}} = 16\), suy ra \({\rm{OH}} = 12\) và \({\rm{H}}( - 12;0).\)
Suy ra những điểm ( \(x\); y) thuộc cung nhỏ AC thoả mãn \({\rm{x}} \in [ - 12;20],{\rm{y}} = \sqrt {400 - {{\rm{x}}^2}} .\)
Hàm số \({\rm{f}}({\rm{x}}) = \sqrt {400 - {{\rm{x}}^2}} ,{\rm{x}} \in [ - 12;20]\) có đồ thị là cung nhỏ AC. Thể tích của chiếc mũ là
\({\rm{V}} = \pi \int_{ - 12}^{20} {{{\left( {\sqrt {400 - {{\rm{x}}^2}} } \right)}^2}} {\rm{dx}} = \pi \int_{ - 12}^{20} {\left( {400 - {{\rm{x}}^2}} \right)} {\rm{dx}}\)
\({\rm{V}} = \left. {\pi \left( {400{\rm{x}} - \frac{{{{\rm{x}}^3}}}{3}} \right)} \right|_{ - 12}^{20} = \pi \left( {400.20 - \frac{{{{20}^3}}}{3}} \right) - \pi \left[ {400.( - 12) - \frac{{{{( - 12)}^3}}}{3}} \right]\)
\( = \frac{{16000\pi }}{3} + 4224\pi = \frac{{28672\pi }}{3} \approx 30025\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
\( \approx 30\left( {{\rm{d}}{{\rm{m}}^3}} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận