Cho a > b > 0, chứng minh rằng
a) a2 > ab và ab > a2;
b) a2 > b2 và a3 > b3.
Chú ý: Tính chất "Với a > b > 0 thì a2 > b2 và a3 > b3" thường hay dùng trong nhiều bài toán chứng minh bất đẳng thức.
Cho a > b > 0, chứng minh rằng
a) a2 > ab và ab > a2;
b) a2 > b2 và a3 > b3.
Chú ý: Tính chất "Với a > b > 0 thì a2 > b2 và a3 > b3" thường hay dùng trong nhiều bài toán chứng minh bất đẳng thức.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Vì a > b > 0 nên:
⦁ a . a > b . a hay a2 > ab.
⦁ a . b > b . b hay ab > b2.
Vậy với a > b > 0 thì a2 > ab và ab > a2.
b) Theo câu a ta có:
a2 > ab > b2, suy ra a2 > b2.
Vì a2 > b2 nên:
⦁ a2 . a > b2 . a hay a3 > ab2.
⦁ b2 . a > b2 . b hay ab2 > b3.
Suy ra a3 > ab2 > b3 hay a3 > b3.
Vậy với a > b > 0 thì a3 > b3.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
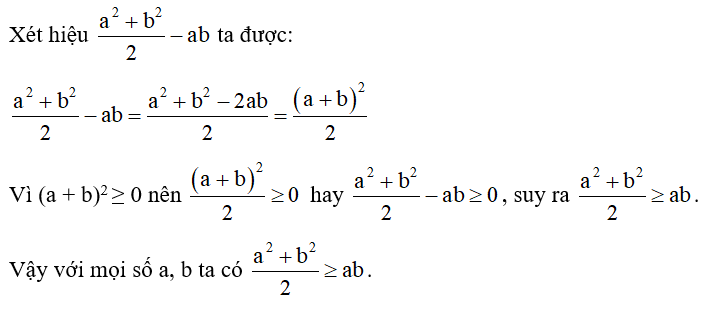
Lời giải
a) Gọi số tuổi của một người là t (tuổi). Để người đó được đi bầu cử đại biểu quốc hội thì t ≥ 18.
b) Gọi x (kg) là khối lượng hàng hóa mà thang máy chở được. Khi đó x ≤ 700.
c) Gọi a (đồng) là số tiền mua hàng. Để được giảm giá thì a ≥ 1 000 000.
d) Gọi y là số bóng được ném vào rổ.
Để được tham gia vào đội tuyển bóng rổ thì y ≥ 5.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập