Gọi AH là đường cao của tam giác ABC vuông tại A. Tính tanABH^ và tanCAH^, suy ra AH2 = BH . CH.

Câu hỏi:

28/09/2024 932

Gọi AH là đường cao của tam giác ABC vuông tại A. Tính $\tan \hat{A B H}$ và $\tan \hat{C A H}$ , suy ra AH² = BH . CH.

Câu hỏi trong đề: Giải SBT Toán 9 KNTT Bài 12. Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Xét tam giác vuông ABH có $\tan \hat{A B H} = \frac{A H}{B H}$ .

Xét tam giác vuông CAH có $\tan \hat{A C H} = \frac{A H}{C H}$ .

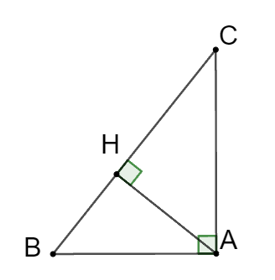
Gọi AH là đường cao của tam giác ABC vuông tại A. Tính góc ABH và góc CAH (ảnh 1)

Vì hai góc BAH và CAH là hai góc phụ nhau (tam giác ABC vuông tại A) nên ta có:

$\tan \hat{A B H} = \cot \hat{A C H} = \frac{1}{\tan \hat{A C H}}$ , hay $\frac{A H}{B H} = \frac{C H}{A H}$ .

Suy ra AH² = BH . CH (đpcm)

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một người đứng xa toà nhà 100 m, dùng giác kế thẳng đứng ngắm thấy điểm trên nóc nhà với góc nhìn 15° (so với phương nằm ngang) (H.4.13). Hỏi toà nhà cao bao nhiêu mét (làm tròn đến chữ số thập phân thứ nhất), biết chiều cao của giác kế là 1,7 m?

Xem đáp án

Lời giải

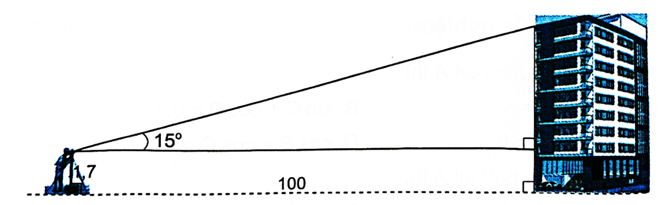
Một người đứng xa toà nhà 100 m, dùng giác kế thẳng đứng ngắm thấy điểm trên (ảnh 2)

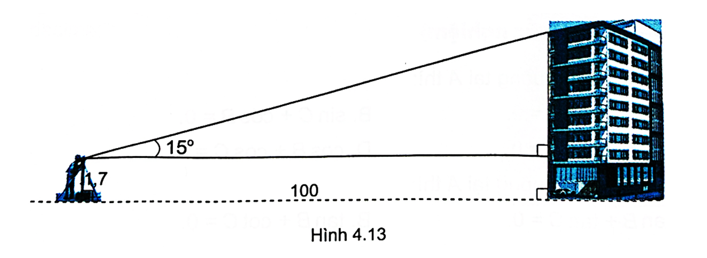
Gọi C là chân tòa nhà, D là điểm trên nóc tòa nhà, A là điểm đặt mắt giác kế.

Kẻ đường cao AH của tam giác ACD, ta có:

CH = 1,7 m, AH = 100 m, $\hat{D A H} = 15 °$ .

Xét tam giác AHD vuông tại H, ta có:

$H D = A H . \tan \hat{D A H} = 100. \tan 15 °$

Do đó CD = CH + HD = 1,7 + 100 . tan 15° ≈ 28,5 (m)

Vậy tòa nhà cao xấp xỉ 28,5 m.

Câu 2

Cho tam giác ABC có BC = 11 cm, $\hat{A B C} = 38 °, \hat{A C B} = 30 ° .$ Gọi H là chân của đường vuông góc kẻ từ A đến BC. Hãy tính AH.

Xem đáp án

Lời giải

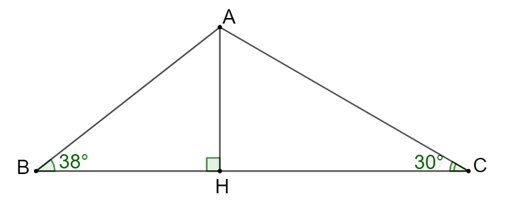
Cho tam giác ABC có BC = 11 cm,góc ABC = 38 độ , góc ACB = 30 độ . Gọi H là chân (ảnh 1)

Vì hai góc B và C của tam giác ABC đều nhọn nên đường cao AH có chân đường cao H nằm giữa B và C.

Gọi h (cm) là độ dài đường cao AH của tam giác ABC.

Xét tam giác ABH vuông tại H, ta có:

$\tan \hat{A B H} = \frac{A H}{B H}$ hay $\tan 38 ° = \frac{h}{B H}$ , suy ra $B H = \frac{h}{\tan 38 °}$ .

Xét tam giác ACH vuông tại H, ta có:

$\tan \hat{A C H} = \frac{A H}{C H}$ hay $\tan 30 ° = \frac{h}{C H}$ , suy ra $C H = \frac{h}{\tan 30 °}$ .

Ta có: $B C = B H + C H$

Hay $11 = \frac{h}{\tan 38 °} + \frac{h}{\tan 30 °} = h (\frac{1}{\tan 38 °} + \frac{1}{\tan 30 °})$

Do đó $h = \frac{11}{\frac{1}{\tan 38 °} + \frac{1}{\tan 30 °}} \approx 3, 652$ (cm).

Vậy AH ≈ 3,652 cm.

Câu 3

Cho tam giác ABC vuông tại A với đường cao AH. Hãy tính cos C theo hai cách và suy ra AC² = BC . HC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Giải tam giác ABC vuông tại A, với AB = c, BC = a, CA = b trong các trường hợp (cạnh làm tròn đến chữ số thập phân thứ ba):

a) a = 5, $\hat{B}$ = 50°;

b) b = 5, $\hat{B}$ = 40°;

c) b = 5, $\hat{C}$ = 55°

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Từ một đài quan sát ở cạnh bờ biển, có độ cao 300 m so với mặt biển, nhìn thấy một con tàu dưới một góc 25° (so với phương nằm ngang của mực nước biển). Hỏi khoảng cách từ tàu đến đài quan sát xấp xỉ bao nhiêu mét?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong một trận chiến đấu, một máy bay của đối phương bay ở độ cao 1 800 m. Khẩu pháo cao xạ ngắm chiếc máy bay đó dưới một góc 35° so với phương nằm ngang. Tìm khoảng cách từ pháo cao xạ đến máy bay (làm tròn đến mét).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Gọi AH là đường cao của tam giác ABC vuông tại A. Tính tanABH^ và tanCAH^, suy ra AH2 = BH . CH.

Cho tam giác ABC có BC = 11 cm, ABC^=38°, ACB^=30°. Gọi H là chân của đường vuông góc kẻ từ A đến BC. Hãy tính AH.

Cho tam giác ABC vuông tại A với đường cao AH. Hãy tính cos C theo hai cách và suy ra AC2 = BC . HC.

Giải tam giác ABC vuông tại A, với AB = c, BC = a, CA = b trong các trường hợp (cạnh làm tròn đến chữ số thập phân thứ ba): a) a = 5, B^ = 50°; b) b = 5, B^ = 40°; c) b = 5, C^ = 55°

Từ một đài quan sát ở cạnh bờ biển, có độ cao 300 m so với mặt biển, nhìn thấy một con tàu dưới một góc 25° (so với phương nằm ngang của mực nước biển). Hỏi khoảng cách từ tàu đến đài quan sát xấp xỉ bao nhiêu mét?

Trong một trận chiến đấu, một máy bay của đối phương bay ở độ cao 1 800 m. Khẩu pháo cao xạ ngắm chiếc máy bay đó dưới một góc 35° so với phương nằm ngang. Tìm khoảng cách từ pháo cao xạ đến máy bay (làm tròn đến mét).

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Gọi AH là đường cao của tam giác ABC vuông tại A. Tính $\tan \hat{A B H}$ và $\tan \hat{C A H}$ , suy ra AH² = BH . CH.

Cho tam giác ABC có BC = 11 cm, $\hat{A B C} = 38 °, \hat{A C B} = 30 ° .$ Gọi H là chân của đường vuông góc kẻ từ A đến BC. Hãy tính AH.

Cho tam giác ABC vuông tại A với đường cao AH. Hãy tính cos C theo hai cách và suy ra AC² = BC . HC.

Giải tam giác ABC vuông tại A, với AB = c, BC = a, CA = b trong các trường hợp (cạnh làm tròn đến chữ số thập phân thứ ba):

a) a = 5, $\hat{B}$ = 50°;

b) b = 5, $\hat{B}$ = 40°;

c) b = 5, $\hat{C}$ = 55°