Giải SBT Toán 9 KNTT Bài 12. Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng có đáp án

65 người thi tuần này 4.6 768 lượt thi 9 câu hỏi

Đề số 1

🔥 Học sinh cũng đã học

84 người thi tuần này

Đề KSCL Toán 9 tháng 10 năm 2026-2027 Trường THCS Từ Liêm 1 (Hà Nội) có đáp án

567 lượt thi 8 câu hỏi

62 người thi tuần này

Đề KSCL Toán 9 tháng 10 năm 2026-2027 Trường THCS Kim Giang (Hà Nội) có đáp án

545 lượt thi 8 câu hỏi

39 người thi tuần này

Đề KSCL Toán 9 tháng 9 năm 2026-2027 Xã Đại Thanh (Hà Nội) có đáp án

522 lượt thi 8 câu hỏi

36 người thi tuần này

Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Hồng Vân (Hà Nội) có đáp án

519 lượt thi 9 câu hỏi

39 người thi tuần này

Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Ngô Sĩ Liên (Hà Nội) có đáp án

522 lượt thi 7 câu hỏi

34 người thi tuần này

Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS&THPT Lương Thế Vinh (Hà Nội) có đáp án

517 lượt thi 8 câu hỏi

30 người thi tuần này

Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Yên Hòa (Hà Nội) có đáp án

513 lượt thi 8 câu hỏi

36 người thi tuần này

Đề KSCL Toán 9 tháng 9 năm 2026-2027 Trường THCS Giảng Võ (Hà Nội) có đáp án

519 lượt thi 10 câu hỏi

Danh sách câu hỏi:

Câu 1/9

Cho tam giác ABC vuông tại A với đường cao AH. Hãy tính cos C theo hai cách và suy ra AC² = BC . HC.

Xem đáp án

Lời giải

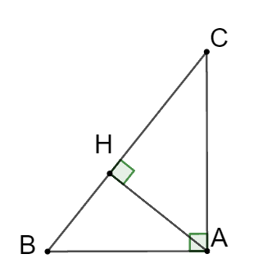
Cho tam giác ABC vuông tại A với đường cao AH. Hãy tính cos C theo hai cách (ảnh 1)

Xét tam giác ABC vuông tại A ta có: $\cos C = \frac{A C}{B C}$ .

Xét tam giác HAC vuông tại H ta có: $\cos C = \frac{H C}{A C}$ .

Suy ra $\frac{A C}{B C} = \frac{H C}{A C}$ , hay AC² = BC . HC (đpcm).

Câu 2/9

Gọi AH là đường cao của tam giác ABC vuông tại A. Tính $\tan \hat{A B H}$ và $\tan \hat{C A H}$ , suy ra AH² = BH . CH.

Xem đáp án

Lời giải

Xét tam giác vuông ABH có $\tan \hat{A B H} = \frac{A H}{B H}$ .

Xét tam giác vuông CAH có $\tan \hat{A C H} = \frac{A H}{C H}$ .

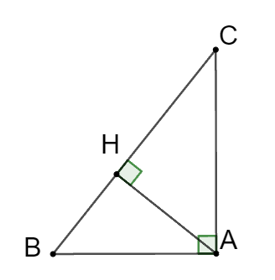
Gọi AH là đường cao của tam giác ABC vuông tại A. Tính góc ABH và góc CAH (ảnh 1)

Vì hai góc BAH và CAH là hai góc phụ nhau (tam giác ABC vuông tại A) nên ta có:

$\tan \hat{A B H} = \cot \hat{A C H} = \frac{1}{\tan \hat{A C H}}$ , hay $\frac{A H}{B H} = \frac{C H}{A H}$ .

Suy ra AH² = BH . CH (đpcm)

Câu 3/9

Cho tam giác ABC vuông tại A, AH là đường cao. Chứng minh rằng $\frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}}$ .

(HD. Ta có sin B = $\frac{A H}{A B}$ , sin C = $\frac{A H}{A C}$ , cos B = sin C và áp dụng công thức sin² α + cos² α = 1 với mọi góc nhọn α).

Xem đáp án

Lời giải

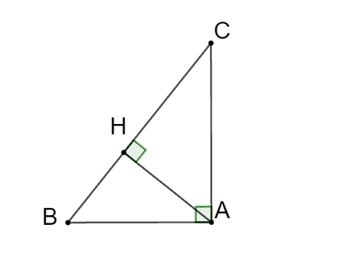
Cho tam giác ABC vuông tại A, AH là đường cao. Chứng minh rằng (ảnh 1)

Xét tam giác ABH vuông tại H, ta có: $\tan \hat{A B H} = \frac{A H}{B H}$ .

Xét tam giác ACH vuông tại H ta có: $\tan \hat{A C H} = \frac{A H}{H C}$ .

Vì $\hat{A B H}$ và $\hat{A C H}$ là hai góc phụ nhau (tam giác ABC vuông tại A) nên:

$\tan \hat{A B H} = \cot \hat{A C H} = \frac{1}{\tan \hat{A C H}}$ hay $\frac{A H}{B H} = \frac{H C}{A H}$ .

Suy ra AH² = BH . CH (đpcm).

Câu 4/9

Cho tam giác ABC có BC = 11 cm, $\hat{A B C} = 38 °, \hat{A C B} = 30 ° .$ Gọi H là chân của đường vuông góc kẻ từ A đến BC. Hãy tính AH.

Xem đáp án

Lời giải

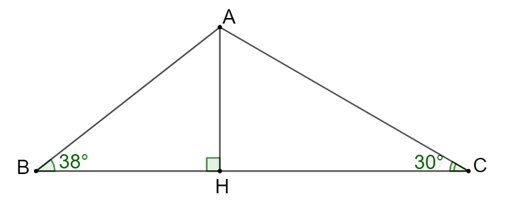
Cho tam giác ABC có BC = 11 cm,góc ABC = 38 độ , góc ACB = 30 độ . Gọi H là chân (ảnh 1)

Vì hai góc B và C của tam giác ABC đều nhọn nên đường cao AH có chân đường cao H nằm giữa B và C.

Gọi h (cm) là độ dài đường cao AH của tam giác ABC.

Xét tam giác ABH vuông tại H, ta có:

$\tan \hat{A B H} = \frac{A H}{B H}$ hay $\tan 38 ° = \frac{h}{B H}$ , suy ra $B H = \frac{h}{\tan 38 °}$ .

Xét tam giác ACH vuông tại H, ta có:

$\tan \hat{A C H} = \frac{A H}{C H}$ hay $\tan 30 ° = \frac{h}{C H}$ , suy ra $C H = \frac{h}{\tan 30 °}$ .

Ta có: $B C = B H + C H$

Hay $11 = \frac{h}{\tan 38 °} + \frac{h}{\tan 30 °} = h (\frac{1}{\tan 38 °} + \frac{1}{\tan 30 °})$

Do đó $h = \frac{11}{\frac{1}{\tan 38 °} + \frac{1}{\tan 30 °}} \approx 3, 652$ (cm).

Vậy AH ≈ 3,652 cm.

Câu 5/9

Giải tam giác ABC vuông tại A, với AB = c, BC = a, CA = b trong các trường hợp (cạnh làm tròn đến chữ số thập phân thứ ba):

a) a = 5, $\hat{B}$ = 50°;

b) b = 5, $\hat{B}$ = 40°;

c) b = 5, $\hat{C}$ = 55°

Xem đáp án

Lời giải

Giải tam giác ABC vuông tại A, với AB = c, BC = a, CA = b trong các trường hợp (ảnh 1)

Giải tam giác ABC vuông tại A, với AB = c, BC = a, CA = b trong các trường hợp (ảnh 2)

Câu 6/9

Cho A, B là hai địa điểm ở hai bên bờ sông, biết AN và PM cùng vuông góc MN, MN = n (mét), MP = p (mét), p > n và $\hat{M P A} = α$ (H.4.12)

Chứng minh rằng: $A B = \frac{p \tan α - n}{\sin α}$

.

Xem đáp án

Lời giải

Vì AN và PM cùng vuông góc với MN nên AN // PM.

Vì AN // PM nên $\hat{B A N} = \hat{B P M} = α$ .

Xét tam giác BAN vuông tại N ta có:

$B N = A B \sin \hat{B A N} = A B . \sin α$

Xét tam giác BPM vuông tại M ta có:

$B M = P M . \tan \hat{B P M} = p . \tan α$

Ta có: BM – BN = MN

p . tan α – AB . sinα = n

AB . sinα = p . tanα – n

$A B = \frac{p . \tan α - n}{\sin α}$ (đpcm).

Câu 7/9

Một người đứng xa toà nhà 100 m, dùng giác kế thẳng đứng ngắm thấy điểm trên nóc nhà với góc nhìn 15° (so với phương nằm ngang) (H.4.13). Hỏi toà nhà cao bao nhiêu mét (làm tròn đến chữ số thập phân thứ nhất), biết chiều cao của giác kế là 1,7 m?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8/9

Trong một trận chiến đấu, một máy bay của đối phương bay ở độ cao 1 800 m. Khẩu pháo cao xạ ngắm chiếc máy bay đó dưới một góc 35° so với phương nằm ngang. Tìm khoảng cách từ pháo cao xạ đến máy bay (làm tròn đến mét).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9/9

Từ một đài quan sát ở cạnh bờ biển, có độ cao 300 m so với mặt biển, nhìn thấy một con tàu dưới một góc 25° (so với phương nằm ngang của mực nước biển). Hỏi khoảng cách từ tàu đến đài quan sát xấp xỉ bao nhiêu mét?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem tiếp với tài khoản VIP

Còn 3/9 câu hỏi, đáp án và lời giải chi tiết.

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Cho tam giác ABC vuông tại A với đường cao AH. Hãy tính cos C theo hai cách và suy ra AC² = BC . HC.

Gọi AH là đường cao của tam giác ABC vuông tại A. Tính $\tan \hat{A B H}$ và $\tan \hat{C A H}$ , suy ra AH² = BH . CH.